
科目: 来源: 题型:
【题目】已知:甲、乙两车分别从相距300千米的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)请直接写出甲、乙两车离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并标明自变量x的取值范围;
(2)它们在行驶的过程中有几次相遇?并求出每次相遇的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC在平面直角坐标系中,且A(-2,1)、B(-3,-2)、C(1,-4).将其平移后得到△A1B1C1,若A,B的对应点是A1,B1,C的对应点C1的坐标是(3,-1).
(1)在平面直角坐标系中画出△ABC和△A1B1C1;
(2)写出点A1的坐标是_____________,B1坐标是___________;
(3)此次平移可看作△ABC向________,平移了____________个单位长度,再向_______平移了______个单位长度得到△A1B1C1.
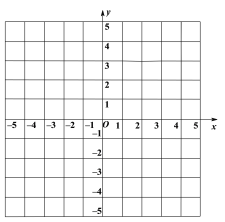
查看答案和解析>>
科目: 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下面的证明:
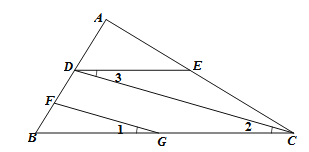
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG//CD (已知)
∴∠2=_________( )
又∵∠1=∠3
∴∠3=∠_________( )
∴BC//__________( )
∴∠B+________=180°( )
又∵∠B=50°
∴∠BDE=130°.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC和△ADE中,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,OA、OC分别是∠PAC和∠PCA的角平分线.


(1)当∠APC =60°时,求∠AOC的度数;
(2)当AB⊥AC,AB=AD=4,AC=3,BC=5时,设AP=x,用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC,∠B=20°时,∠AOC的取值范围为α°<∠AOC <β°,直接写出α、β的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=2AE=4,∠BCE=30°.
(1)求平行四边形ABCD的面积S;
(2)求证:∠EMC=2∠AEM.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AE为边BC上的高,点D为边BC上的一点,连接AD.

(1)当AD为边BC上的中线时.若AE=4,△ABC的面积为24,求CD的长;
(2)当AD为∠BAC的角平分线时.
①若∠C =65°,∠B =35°,求∠DAE的度数;
②若∠C-∠B =20°,则∠DAE = °.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).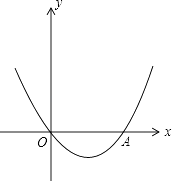
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】请认真观察图形,解答下列问题:

(1)根据图中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1: ;
方法2: .
(2)从中你能发现什么结论,请用等式表示出来: ;
(3)利用(2)中结论解决下面的问题:若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com