
科目: 来源: 题型:
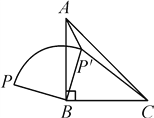
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )
A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.

(1)求证:AE=BC;
(2)如图(2),过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到△AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知![]() ,点
,点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的两点.将射线
上的两点.将射线![]() 绕点
绕点![]() 顺时针匀速旋转,将射线
顺时针匀速旋转,将射线![]() 绕点
绕点![]() 顺时针匀速旋转,旋转后的射线分别记为
顺时针匀速旋转,旋转后的射线分别记为![]() 、
、![]() ,已知射线
,已知射线![]() 、射线
、射线![]() 旋转的速度之和为6度/秒.
旋转的速度之和为6度/秒.

(1)射线![]() 先转动
先转动![]() 得到射线
得到射线![]() ,然后射线
,然后射线![]() 、
、![]() 再同时旋转10秒,此时射线
再同时旋转10秒,此时射线![]() 与射线
与射线![]() 第一次出现平行.求射线
第一次出现平行.求射线![]() 、
、![]() 的旋转速度;
的旋转速度;
(2)若射线![]() 、
、![]() 分别以(1)中速度同时转动
分别以(1)中速度同时转动![]() 秒,在射线
秒,在射线![]() 与射线
与射线![]() 重合之前,设射线
重合之前,设射线![]() 与射线
与射线![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,如图2所示.
,如图2所示.
①当![]() 时,求
时,求![]() 、
、![]() 、
、![]() 满足的数量关系;
满足的数量关系;
②当![]() 时,求
时,求![]() 和
和![]() 满足的数量关系.
满足的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】猜想与证明:小强想证明下面的问题:“有两个角(图中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的
)相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的![]() 和边
和边![]() .
.
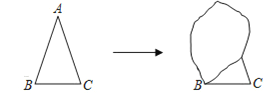
(1)请问:他能够把图恢复成原来的样子吗?若能,请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子.

(2)你能够证明这样的三角形是等腰三角形吗?(至少用两种方法证明)

查看答案和解析>>
科目: 来源: 题型:
【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
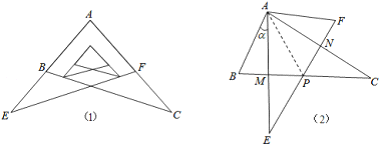
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段![]() 和折线
和折线![]() 表示“龟兔赛跑”时路程与时间的关系.请你根据图中给出的信息,解决下列问题.
表示“龟兔赛跑”时路程与时间的关系.请你根据图中给出的信息,解决下列问题.

(1)填空:折线![]() 表示赛跑过程中__________的路程与时间的关系,线段
表示赛跑过程中__________的路程与时间的关系,线段![]() 表示赛跑过程中__________的路程与时间的关系;
表示赛跑过程中__________的路程与时间的关系;
(2)兔子在起初每分钟跑多少千米?乌龟每分钟爬多少米?
(3)兔子醒来后,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子在途中一共睡了多少分钟?
查看答案和解析>>
科目: 来源: 题型:
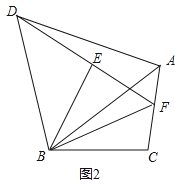
【题目】将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF.
(1)如图1,若∠ABC=α=60°,BF=AF.
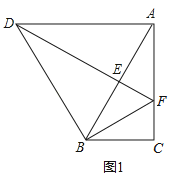
①求证:DA∥BC;②猜想线段DF、AF的数量关系,并证明你的猜想;
(2)如图2,若∠ABC<α,BF=mAF(m为常数),求![]() 的值(用含m、α的式子表示).
的值(用含m、α的式子表示).
查看答案和解析>>
科目: 来源: 题型:
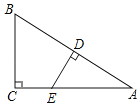
【题目】如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AB,AC于点D,E.
(1)求证:AE=2CE;
(2)当DE=1时,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】(12分)如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D,旋转角为![]() .
.
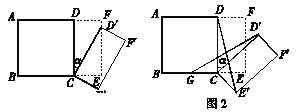
(1)当点D′恰好落在EF边上时,则旋转角α的值为________度;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,是否存在旋转角α,使△DCD′与△CBD′全等?若能,直接写出旋转角α的值;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com