
科目: 来源: 题型:
【题目】如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:

(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)按(1)中的直角坐标系在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是______,△ABC的面积是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目: 来源: 题型:
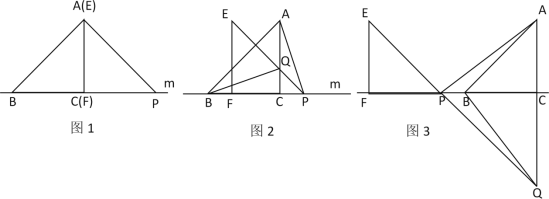
【题目】(1)问题情境,如图1,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△EFP的边FP也在直线m上,边EF与边AC重合,且EF=FP,
在图1中,AB与AP的数量关系是_______,AB与AP的位置关系是_______
(2)操作发现:将△EFP沿直线m向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并证明BQ与AP的数量关系和位置关系
(3)猜想论证:将△EFP沿直线m向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,(2)中的结论还成立吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE,
(1)求证:AE=AC
(2)若∠AEC=60°,将△ADE绕点A逆时针旋转后与△ABC重合,则这个旋转角的度数__
(3)若AC=4,BC=7,∠AEC=60°,求△ABE的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.

(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan53°≈1.33, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目: 来源: 题型:
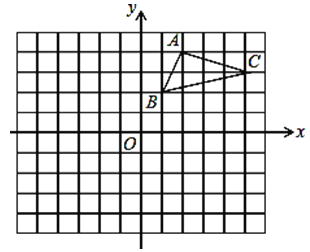
【题目】在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4)
(1)画出△ABC先向左平移1个单位,再向下平移4个单位得到的△A1B1C1,写出点A1的坐标____________
(2)画出△A1B1C1绕原点O顺时针旋转90°,得到△A2B2C2,写出点A2的坐标_______
查看答案和解析>>
科目: 来源: 题型:
【题目】探究思考:(本题直接填空,不必写出解题过程)
问题:在数轴上,点A表示的数为![]() ,则到点A的距离等于3的点所表示的数是 ;
,则到点A的距离等于3的点所表示的数是 ;
变式思考一:如图1,在数轴上有六个点A、B、C、D、E、F,且相邻两点间距离相等,若点A表示的数是![]() ,点F表示的数为11,则与点C表示的数最近的整数是 ;
,点F表示的数为11,则与点C表示的数最近的整数是 ;
![]()
变式思考二:已知数轴上有A、B、C三点,分别代表![]() ,电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到 秒时,电子蚂蚁到A、B、C的距离和为40个单位.
,电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到 秒时,电子蚂蚁到A、B、C的距离和为40个单位.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面文字:
对于(﹣5![]() )+(﹣9
)+(﹣9![]() )+17
)+17![]() +(﹣3
+(﹣3![]() )
)
可以如下计算:
原式=[(﹣5)+(﹣![]() )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣![]() )]+(17+
)]+(17+![]() )+[(﹣3)+(﹣
)+[(﹣3)+(﹣![]() )]
)]
=[(一5)+(﹣9)+17+(一3)]+[(﹣![]() )+(﹣
)+(﹣![]() )+
)+![]() +(﹣
+(﹣![]() )]=0+(﹣1
)]=0+(﹣1![]() )
)
=﹣1![]()
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1![]() )+(﹣2000
)+(﹣2000![]() )+4000
)+4000![]() +(﹣1999
+(﹣1999![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com