
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出以下结论:①abc<0;②b2-4ac>0;③4b+c<0;④若B(-![]() ,y1),C(-
,y1),C(-![]() ,y2)为函数图象上的两点,则y1>y2;⑤当-3≤x≤1时,y≥0,其中正确的结论是______.(填序号)
,y2)为函数图象上的两点,则y1>y2;⑤当-3≤x≤1时,y≥0,其中正确的结论是______.(填序号)

查看答案和解析>>
科目: 来源: 题型:
【题目】把一副三角板如图放置 其中∠ACB=∠DEC=90,∠A=45,∠D=30,斜边 AB=4,CD=5,把三角板DCE绕点C顺时针旋转15得到三角形D1CE (如图二),此时AB与CD1交于点O,则线段AD1的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点C运动;点Q以1.25cm/s的速度沿BC向终点C运动,两点到达终点后停止运动。过点P作PE∥BC交AD于点E,连结EQ,设动点运动的时间为ts(t>0)。
(1) 连结DP,经过1s后,四边形EQDP能够成为平行四边形吗? 请说明理由;
(2) 当t为何值时,△EDQ为直角三角形?
(3) 如图②,设点M是EQ的中点,在点P、Q的整个运动过程中,试探究点M的运动路径长度是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】我校七年级某班准备买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副![]() 元,乒乓球每盒
元,乒乓球每盒![]() 元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的
元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的![]() 折优惠这个班级需要球拍
折优惠这个班级需要球拍![]() 副,乒乓球
副,乒乓球![]() 盒(
盒(![]() ).
).
(1)分别求甲、乙两家商店购买这些商品所箭的费用(用含x的代数式表示);
(2)当![]() 时,购买所需商品去哪家商店合算?请通过计算说明理由.
时,购买所需商品去哪家商店合算?请通过计算说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,从①AB//CD;②AB=CD;③BC//AD;④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有哪几种,请一一写出_____________.

查看答案和解析>>
科目: 来源: 题型:
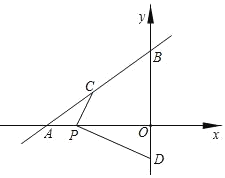
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
(1)点C的坐标为 ,点D的坐标为 ;
(2)点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
查看答案和解析>>
科目: 来源: 题型:
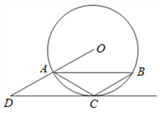
【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB,CD与OA的延长线交于点D.
(1)求证:CD 是⊙O 的切线;
(2)若∠ACB=120°,OA=2,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com