
科目: 来源: 题型:
【题目】把下列各数填在相应的大括号里:
1,﹣![]() ,8.9,﹣7,
,8.9,﹣7, ![]() ,﹣3.2,+1 008,﹣0.06,28,﹣9.
,﹣3.2,+1 008,﹣0.06,28,﹣9.
正整数集合:{______…};
负整数集合:{______…};
正分数集合:{______…};
负分数集合:{______…}.
查看答案和解析>>
科目: 来源: 题型:
【题目】宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
(约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
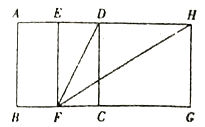
A. 矩形ABFE B. 矩形EFCD C. 矩形EFGH D. 矩形DCGH
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A,B,C三点在数轴上,点A表示的数为-10,点B表示的数为14,点C到点A和点B之间的距离相等.
![]()
(1)求A,B两点之间的距离;
(2)求C点对应的数;
(3)甲、乙分别从A,B两点同时相向运动,甲的速度是1个单位长度/s,乙的速度是2个单位长度/s,求相遇点D对应的数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△OAB与△OCD是以点0为位似中心的位似图形,相似比为1:2,∠OCD=90![]() ,CO=CD.若B(2,0),则点C的坐标为( )
,CO=CD.若B(2,0),则点C的坐标为( )
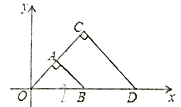
A. (2,2) B. (1,2) C. (![]() ,2
,2![]() ) D. (2,1)
) D. (2,1)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数![]() 的图象过点A(0,3)和点B(3,0),且与正比例函数
的图象过点A(0,3)和点B(3,0),且与正比例函数![]() 的图象交于点P.
的图象交于点P.
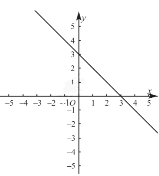
(1)求函数![]() 的解析式和点P的坐标.
的解析式和点P的坐标.
(2)画出两个函数 的图象,并直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
(3)若点Q是![]() 轴上一点,且△PQB的面积为8,求点Q的坐标.
轴上一点,且△PQB的面积为8,求点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为
点对应的数为![]() ,
,![]() 点对应的数为
点对应的数为![]() .
.
![]()
(1)请写出与![]() 、
、![]() 两点距离相等的点
两点距离相等的点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚁![]() 从
从![]() 点出发,以
点出发,以![]() 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以
点出发,以![]() 单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,你知道
点相遇,你知道![]() 点对应的数是多少吗?(写出计算过程)
点对应的数是多少吗?(写出计算过程)
(3)在题(2)中,若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】高高地路灯挂在路边的上方,高傲而明亮,小明拿着一根![]() 米长的竹竿,想量一量路灯的高度,直接量是不可能的,于是,他走到路灯旁的一个地方,竖起竹竿,这时,他量了一下竹竿的影长正好是
米长的竹竿,想量一量路灯的高度,直接量是不可能的,于是,他走到路灯旁的一个地方,竖起竹竿,这时,他量了一下竹竿的影长正好是![]() 米,他沿着影子的方向走,向远处走出两根竹竿的长度(即
米,他沿着影子的方向走,向远处走出两根竹竿的长度(即![]() 米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即
米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即![]() 米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,原来路灯有
米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,原来路灯有![]() 米高呀!”(如图所示)同学们,你觉得小明的判断对吗?
米高呀!”(如图所示)同学们,你觉得小明的判断对吗?
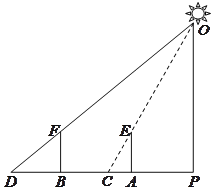
查看答案和解析>>
科目: 来源: 题型:
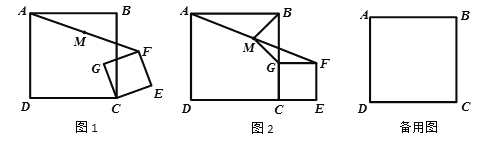
【题目】如图1,正方形CEFG绕正方形ABCD的顶点C旋转,连接AF,点M是AF中点.
(1)当点G在BC上时,如图2,连接BM、MG,求证:BM=MG;
(2)在旋转过程中,当点B、G、F三点在同一直线上,若AB=5,CE=3,则MF= ;
(3)在旋转过程中,当点G在对角线AC上时,连接DG、MG,请你画出图形,探究DG、MG的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数分别填入相应的大括号里:
-6, 9.3,![]() ,42,0,-0.33,0.333…,1.41421356,-2π,3.3030030003…,-3.1415926.
,42,0,-0.33,0.333…,1.41421356,-2π,3.3030030003…,-3.1415926.
正数集合{ };
负数集合{ };
有理数集合{ };
无理数集合{ }.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com