
科目: 来源: 题型:
【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,![]() ,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
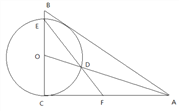
(1)求证:AB是⊙O的切线;
(2)求![]() 的值。
的值。
(3)若⊙O的半径为4,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
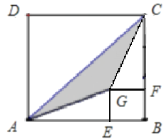
【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
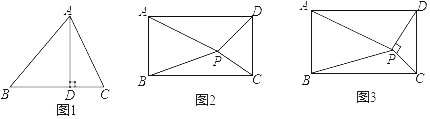
【题目】(几何背景)如图1,AD为锐角△ABC的高,垂足为D.求证:AB2﹣AC2=BD2﹣CD2
(知识迁移)如图2,矩形ABCD内任意一点P,连接PA、PB、PC、PD,请写出PA、PB、PC、PD之间的数量关系,并说明理由.
(拓展应用)如图3,矩形ABCD内一点P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c满足a2﹣b2=![]() c2,则
c2,则![]() 的值为 (请直接写出结果)
的值为 (请直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】“低碳生活,绿色出行”,共享单车已经成了很多人出行的主要选择,今年1月份,“摩拜”共享单车又向长沙河西新投放共享单车640辆.
(1)若1月份到3月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.求月平均增长率。
(2)考虑到共享单车市场竞争激烈,摩拜公司准备用不超过60000元的资金再购进A,B两种规格的自行车100辆,且A型车不超过60辆。已知A型的进价为500元/辆,B型车进价为700元/辆,设购进A型车m辆,求出m的取值范围。
(3)已知A型车每月产生的利润是100元/辆,B型车每月产生的利润是90元/辆,在(2)的条件下,求公司每月的最大利润。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn,你认为其中正确的有( )

A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的材料:
点A、B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|
当A、B两点中有一点在原点时,设点A在原点,如图①|AB|=|OB|=|b|=|a﹣b|
当A、B两点都不在原点时,

(1)如图②,点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图③,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|
(3)如图④,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|
综上所述,数轴上A、B两点之间的距离|AB|=|a﹣b|
请用上面的知识解答下面的问题:
(1)数轴上表示﹣2和﹣4的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 .
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 .
(3)当|x+1|+|x﹣2|=5时的整数x的值 .
(4)当|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某公安海上缉私局发现在我国领海的P处有一条走私船正以22海里/时的速度沿南偏东64的方向向公海逃窜,于是缉私局命令位于点P北偏东30方向A处的我公安缉私快艇前往拦截,已知P、A相距20海里,公安缉私快艇向正南方向行进计划在B处拦截走私船。
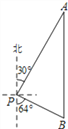
(1)求A、B两处的距离;(结果保留整数)
(2)若公安缉私快艇要在B处成功拦截走私船,则缉私快艇的速度至少为多少海里/时?
【参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2,![]() ,
,![]() ,
,![]() 】
】
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,在九年级随机抽取了一部分学生 的期末数学成绩为样本,分为 A(90~100 分);B(80~89 分);C(60~79 分);D(0~59 分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下 问题.
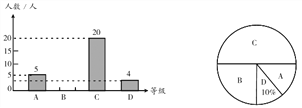
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生 1200 人,若分数为 80 分(含 80 分)以上为优秀,请估 计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目: 来源: 题型:
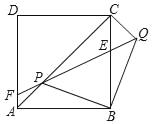
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
查看答案和解析>>
科目: 来源: 题型:
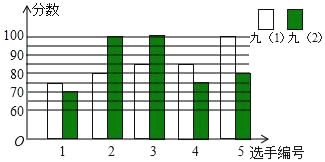
【题目】为选拔优秀选手参加瑶海区第八届德育文化艺术节“诵经典”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示
(1)根据图示填写下表
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 |
| 85 |
九(2) |
| 80 |
|
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班五名选手的成绩较稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com