
科目: 来源: 题型:
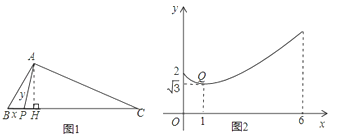
【题目】在△ABC中,AH⊥BC于点H,点P从B点开始出发向C点运动,在运动过程中,设线段AP的长为y,线段BP的长为x(如图1),而y关于x的函数图象如图2所示.Q (1,![]() )是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=
)是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=![]() ;③AC=2
;③AC=2![]() ;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是________(填写序号).
;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是________(填写序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
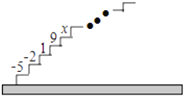
(尝试)(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数![]() 是多少?
是多少?
(应用)求从下到上前33个台阶上数的和.
(发现)试用含![]() (
(![]() 为正整数)的式子表示出数“-2”所在的台阶数(此问直接写出结果).
为正整数)的式子表示出数“-2”所在的台阶数(此问直接写出结果).
查看答案和解析>>
科目: 来源: 题型:
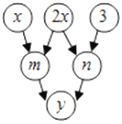
【题目】如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
示例: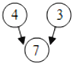 即
即![]()
则(1)用含![]() 的式子表示
的式子表示![]() ______;
______;
(2)当![]() 时,
时,![]() ______,
______,![]() 的值为______.
的值为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起,催生了快递行业的高速发展.据调查,杭州市某家小型快递公司,今年一月份与三月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率;
(2)如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:数x、y、z中较大的数称为max{x,y,z}.例如max{﹣3,1,﹣2}=1,函数y=max{﹣t+4,t,![]() }表示对于给定的t的值,代数式﹣t+4,t,
}表示对于给定的t的值,代数式﹣t+4,t,![]() 中值最大的数,如当t=1时y=3,当t=0.5时,y=6.则当t=_________时函数y的值最小.
中值最大的数,如当t=1时y=3,当t=0.5时,y=6.则当t=_________时函数y的值最小.
查看答案和解析>>
科目: 来源: 题型:
【题目】一销售员向某企业推销一种该企业生产必需的物品,若企业要40件,则销售员每件可获利40元,销售员(在不亏本的前提下)为扩大销售量,而企业为了降低生产成本,经协商达成协议,如果企业购买40件以上时,每多要1件,则每件降低1元.
(1)设每件降低![]() (元)时,销售员获利为
(元)时,销售员获利为![]() (元),试写出
(元),试写出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)当每件降低20元时,问此时企业需购进物品多少件?此时销售员的利润是多少?
查看答案和解析>>
科目: 来源: 题型:
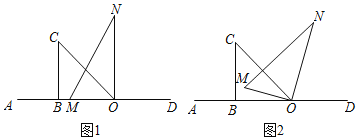
【题目】将一副直角三角板按如图1摆放在直线AD上![]() 直角三角板OBC和直角三角板MON,
直角三角板OBC和直角三角板MON,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板OBC不动,将三角板MON绕点O以每秒
,保持三角板OBC不动,将三角板MON绕点O以每秒![]() 的速度顺时针方向旋转t秒
的速度顺时针方向旋转t秒![]()
![]() 如图2,
如图2,![]() ______度
______度![]() 用含t的式子表示
用含t的式子表示![]() ;
;
![]() 在旋转的过程中,是否存在t的值,使
在旋转的过程中,是否存在t的值,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒
直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒![]() 的速度顺时针旋转.
的速度顺时针旋转.
![]() 当
当![]() ______秒时,
______秒时,![]() ;
;
![]() 请直接写出在旋转过程中,
请直接写出在旋转过程中,![]() 与
与![]() 的数量关系
的数量关系![]() 关系式中不能含
关系式中不能含![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过部分按每吨1.8元收费,该市某户居民5月份用水![]() 吨
吨![]() ,应缴水费
,应缴水费![]() 元.
元.
(1)写出![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)某户居民若5月份用水16吨,应缴水费多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (p,q是正整数,且
(p,q是正整数,且![]() ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为![]() ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
(3)在(2)所得“和谐数”中,求F(t)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com