
科目: 来源: 题型:
【题目】如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
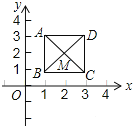
A. (﹣2012,2)B. (﹣2012,﹣2)C. (﹣2013,﹣2)D. (﹣2013,2)
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴上.
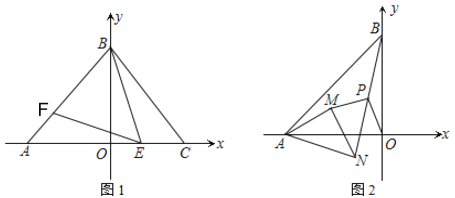
(1)如图1,点A与点C关于y轴对称,点E、F分别是线段AC、AB上的点(点E不与点A、C重合),且∠BEF=∠BAO.若∠BAO=2∠OBE,求证:AF=CE;
(2)如图2,若OA=OB,在点A处有一等腰△AMN绕点A旋转,且AM=MN,∠AMN=90°.连接BN,点P为BN的中点,试猜想OP和MP的数量关系和位置关系,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:
(阅读材料)
在数轴上,通常用“两数的差”来表示“数轴上两点的距离”如图1中三条线段的
长度可表示为:![]() ,
,![]() 结论:数轴上任意两点
结论:数轴上任意两点
表示的数为分别![]() ,则这两个点间的距离为
,则这两个点间的距离为![]() (即:用较大的数去减较小的数)
(即:用较大的数去减较小的数)
![]()
(理解运用)
根据阅读材料完成下列各题:
(1)如图2, ![]() 分别表示数
分别表示数![]() ,求线段
,求线段![]() 的长;
的长;
![]()
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 对应的数值.
对应的数值.
(3)![]() 两点分别从
两点分别从![]() 同时出发以3个单位、2个单位长度的速度沿数轴向右运动,求当点
同时出发以3个单位、2个单位长度的速度沿数轴向右运动,求当点![]() 重合时,它们运动的时间;
重合时,它们运动的时间;
(4)在(3)的条件下,求当![]() 时,它们运动的时间.
时,它们运动的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果商店以每箱200元价格从市场上购进一批苹果共8箱,若以每箱苹果净重
30千克为标准,超过千克数记为正数,不足千克数记为负数,称重后记录如下:
![]()
(1)这8箱苹果一共中多少千克,购买这批苹果一共花了多少钱?
(2)若把苹果的销售单价定为每千克![]() 元,那么销售这批苹果(损耗忽略不计)获得的总销售金额为_____元,获得利润为____________元(用含字母
元,那么销售这批苹果(损耗忽略不计)获得的总销售金额为_____元,获得利润为____________元(用含字母![]() 的式子表示);
的式子表示);
(3)在(2)条件下,若水果商店计划共获利![]() ,请你通过列方程并求出
,请你通过列方程并求出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明遇到这样一个问题,如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC.求∠C的度数。小明通过探究发现,延长CD至点Q,使BQ=AB,再证明△ADC≌△ADQ,使问题得到解决.

(1)根据阅读材料回答,△ADC≌△ADQ的条件是________(填SSS,SAS,AAS,ASA,或HL)
(2)参考小明思考问题的方法,解答下列问题:求∠C的度数;
(3)解决问题,如图,已知,△ABC中,过点B任意作射线l,在l上取一点D,使∠ABD=∠ACD,AM⊥BD于点M,且BM=MD+CD。探究AB与AC的数量关系,并证明.

查看答案和解析>>
科目: 来源: 题型:
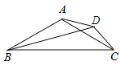
【题目】如图:等腰△ABC中,AB=AC,点D在AC右侧,∠BAC=∠BDC=120°
(1)猜想DA,DC,DB的数量关系并证明
(2)点D 在AB边左侧时三条线段关系是否发生变化?请画出图形。若变化,直接写出结论.
查看答案和解析>>
科目: 来源: 题型:
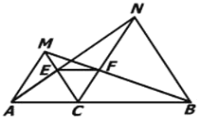
【题目】已知:如图,点C为线段AB上一点,△ACM, △CBN都是等边三角形,AM=AC=CM,BC=CN=BN,∠ACM=∠BCN=60°,AN交MC于点E,BM交CN于点F.
(1)求证:AN=BM;
(2)求证:判断△CEF形状
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下列菱形的摆放规律,解答下列问题.
(1)如图:
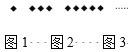
按此规律,图4有____个菱形,若第![]() 个图形有35个菱形,则
个图形有35个菱形,则![]() ___________;
___________;
(2)如图:

按此规律,图5有______个菱形,若第![]() 个图形有___个菱形(用含
个图形有___个菱形(用含![]() 的式子表示).
的式子表示).
(3)如图:
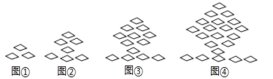
按此规律图6有________个菱形,第![]() 个图形中有__________个菱形(用含的式子表示).
个图形中有__________个菱形(用含的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com