
科目: 来源: 题型:
【题目】已知关于x的方程![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 当k=0时,方程没有实数根 B. 当k=1时,方程有一个实数根
C. 当k=-1时,方程有两个相等的实数根 D. 当k≠0时,方程总有两个不相等的实数根
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是( )
CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是( )
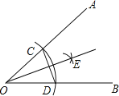
A.△OCD是等腰三角形B.CD垂直平分OE
C.点E到OA、OB的距离相等D.证明射线OE是角平分线的依据是SSS
查看答案和解析>>
科目: 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,长方形AOCB的顶点A(m,n)和C(p,q)在坐标轴上,已知![]() 和
和![]() 都是方程x+2y=4的整数解,点B在第一象限内.
都是方程x+2y=4的整数解,点B在第一象限内.
(1)求点B的坐标;
(2)若点P从点A出发沿y轴负半轴方向以1个单位每秒的速度运动,同时点Q从点C出发,沿x轴负半轴方向以2个单位每秒的速度运动,问运动到多少秒时,四边形BPOQ面积为长方形ABCO面积的一半;
(3)如图2,将线段AC沿x轴正方向平移得到线段BD,点E(a,b)为线段BD上任意一点,试问a+2b的值是否变化?若变化,求其范围;若不变化,求其值.(直接写出结论)

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
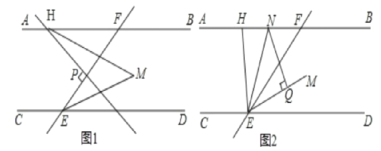
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
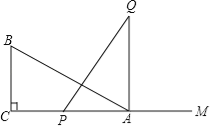
查看答案和解析>>
科目: 来源: 题型:
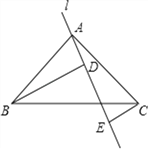
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com