【题目】阅读材料：我们知道：点A．B在数轴上分别表示有理数a、b，A．B两点之间的距离表示为AB，在数轴上A．B两点之间的距离AB=|a-b|．所以式子|x3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离．

【题目】在同一平面直角坐标系中，函数y＝ax2＋b与y＝bx2＋ax的图象可能是(　　)

【题目】如图,直线l是矩形ABCD的一条对称轴,AD=2AB,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有( )个.

【题目】在矩形ABCD中，AB＝4，AD＝3，矩形内部有一动点P满足S矩形ABCD＝3S△PAB，则PA+PB的最小值为_____．

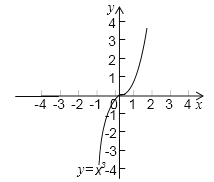
【题目】利用图象解一元二次方程x2－2x－1＝0时，我们采用的一种方法是在直角坐标系中画出抛物线y＝x2和直线y＝2x＋1，两图象交点的横坐标就是该方程的解．

【题目】如图所示，有一座抛物线形拱桥，桥下面在正常水位时，AB宽20 m，水位上升到警戒线CD时，CD到拱桥顶E的距离仅为1 m，这时水面宽度为10 m.

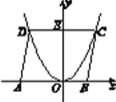
【题目】如图所示，已知函数y＝ax2(a≠0)的图象上的点D，C与x轴上的点A(－5，0)和B(3，0)构成ABCD，DC与y轴的交点为E(0，6)，试求a的值．

【题目】已知一列数：1，－2，3，－4，5，－6，7…将这列数排成下列形式：

【题目】已知二次函数y＝x2+mx+n的图象经过点P（﹣3，1），对称轴是直线x＝﹣1．