
科目: 来源: 题型:
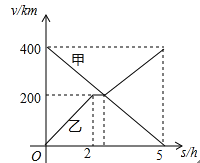
【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)乙车休息了 h;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;
(3)当两车相距40km时,直接写出x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+2(a≠0)的图象与x 轴交于A,B 两点,与y 轴交于点C,已知点 A(-4,0),B(1,0).
(1)求抛物线的解析式;
(2)若点 D(m,n) 是抛物线在第二象限的部分上的一动点,四边形 ![]() 的面积为
的面积为 ![]() ,求
,求 ![]() 关于 m 的函数关系;
关于 m 的函数关系;
(3)若点 E 为抛物线对称轴上任意一点,当以 A,C,E 为顶点的三角形是直角三角形时,请求出满足条件的所有点 E 的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】正方形ABCD的边长为6cm,点E,M分别是线段BD,AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图①,若点M与点D重合,求证:AF=MN;
(2)如图②,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以![]() cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.
①设BF=ycm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,A(-4,0),B(6,0),C(2,4),D(-3,2).
(1)求四边形ABCD的面积;
(2)在y轴上找一点P,使△APB的面积等于四边形的一半,求P点坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】2019 年 4 月 27 日,第二届“一带一路”国际合作高峰论坛圆满闭幕.“一带一路”已成为我国参与全球开放合作、改善全球经济治理体系、促进全球共同发展繁荣、推动构建人类命运共同体的中国方案.其中中欧班列见证了“一带一路”互联互通的跨越式发展,年运送货物总值由 2011 年的不足 6 亿美元,发展到 2018 年的约 160 亿美元.下面是 2011-2018 年中欧班列开行数量及年增长率的统计图.
根据图中提供的信息填空:

(1)2018 年,中欧班列开行数量的增长率是_____;
(2)如果 2019 年中欧班列的开行数量增长率不低于 50%,那么 2019 年中欧班列开行数量至少是_____列.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校购买一批办公用品,有甲、乙两家超市可供选择:甲超市给予每件0.8元的优惠价格,乙商超市的优惠条件如图象所示.

(1)分别求出在两家超市购买费用 y(元)与购买数量x(件)的函数关系式;
(2)若你是学校采购员,应如何选择才能更省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】下面两个统计图反映的是甲、乙两所学校三个年级的学生在各校学生总人数中的占比情况,下列说法错误的是( )
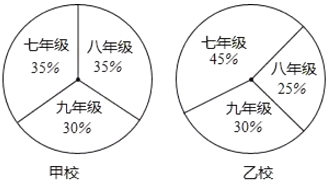
A.甲校中七年级学生和八年级学生人数一样多B.乙校中七年级学生人数最多
C.乙校中八年级学生比九年级学生人数少D.甲、乙两校的九年级学生人数一样多
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点D为△ABC边BC的延长线上一点.

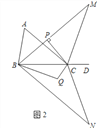
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证: ![]() ;
;
(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进![]() 种型号衣服9件,
种型号衣服9件,![]() 种型号衣服10件,则共需1810元;若购进
种型号衣服10件,则共需1810元;若购进![]() 种型号衣服12件,
种型号衣服12件,![]() 种型号衣服8件,共需1880元;已知销售一件
种型号衣服8件,共需1880元;已知销售一件![]() 型号衣服可获利18元,销售一件
型号衣服可获利18元,销售一件![]() 型号衣服可获利30元.要使在这次销售中获利不少于699元,且
型号衣服可获利30元.要使在这次销售中获利不少于699元,且![]() 型号衣服不多于28件.
型号衣服不多于28件.
(1)求![]() 型号衣服进价各是多少元?
型号衣服进价各是多少元?
(2)若已知购进![]() 型号衣服是
型号衣服是![]() 型号衣服的2倍还多4件,则商店在这次进货中可有几种方案?并简述购货方案.
型号衣服的2倍还多4件,则商店在这次进货中可有几种方案?并简述购货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com