
科目: 来源: 题型:
【题目】已知,如图,在 ABC 中, ACB 90, B 60, BC 2 ,MON 30.
(1)如图 1, MON 的边 MO ⊥ AB ,边 ON 过点 C ,求 AO 的长;
(2)如图 2,将图 1 中的 MON 向右平移,MON 的两边分别与 ABC 的边 AC 、BC
相交于点 E 、 F ,连接 EF ,若 OEF 是直角三角形,求 AO 的长;
(3)在(2)的条件下,MON 与 ABC 重叠部分面积是否存在最大值,若存在,求出 最大值,若不存在,请说明理由.
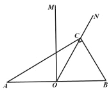
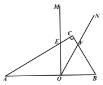
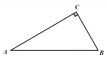
图 1 图 2 备用图
查看答案和解析>>
科目: 来源: 题型:
【题目】三角形内角和定理告诉我们:三角形三个内角的和等于180°.如何证明这个定理呢?
我们知道,平角是180°,要证明这个定理就是把三角形的三个内角转移到一个平角中去,请根据如下条件,证明定理.
(定理证明)
已知:△ABC(如图①).
求证:∠A+∠B+∠C=180°.
(定理推论)如图②,在△ABC中,有∠A+∠B+∠ACB=180°,点D是BC延长线上一点,由平角的定义可得∠ACD+∠ACB=180°,所以∠ACD= .从而得到三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
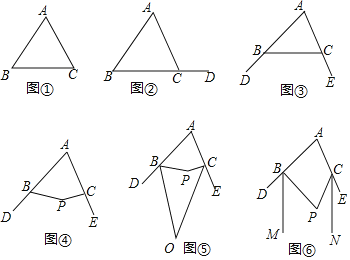
(初步运用)如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=80°,∠DBC=150°,则∠ACB= ;
(2)若∠A=80°,则∠DBC+∠ECB= .
(拓展延伸)如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=80°,∠P=150°,则∠DBP+∠ECP= ;
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=50°,则∠A和∠P的数量关系为 ;
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果自然数m使得作竖式加法![]() 时对应的每个数位都不产生进位,则称m为“幸运数”.
时对应的每个数位都不产生进位,则称m为“幸运数”.
例如:12,321都是“幸运数”,理由是12+13+14及321+322+323每个数位都不产生进位;50,123都不是“幸运数”,理由是50+51+52及123+124+125十位或个位分别产生了进位.
(1)判断2019和2020是否是“幸运数”?请说明理由;
(2)求出三位数中小于200且是3的倍数的“幸运数”.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图 1,在平面直角坐标系中,图形 W在坐标轴上的投影长度定义如下:设点 P(![]() ,
, ![]() ) ,Q(
) ,Q(![]() ,
, ![]() ) 是图形 W 上的任意两点,若
) 是图形 W 上的任意两点,若![]() 的最大值为 m ,则
的最大值为 m ,则
图形 W 在 x 轴上的投影长度为 lx m ;若![]() 的最大值为 n ,则图形 W 在 y 轴上的
的最大值为 n ,则图形 W 在 y 轴上的
投影长度为 ly n .如图 1,图形 W 在 x 轴上的投影长度为 lx ![]() 4 ;在 y 轴上的 投影长度为 ly
4 ;在 y 轴上的 投影长度为 ly ![]() 3 .
3 .
(1)已知点 A(1, 2) , B(2, 3) , C (3,1) ,如图 2 所示,若图形 W 为四边形 OABC ,
则 lx , ly ;
(2)已知点 C (![]() , 0) ,点 D 在直线 y
, 0) ,点 D 在直线 y ![]() x 1(x 0) 上,若图形 W 为 OCD ,当 lx ly
x 1(x 0) 上,若图形 W 为 OCD ,当 lx ly
时,求点 D 的坐标;
(3 )若图形 W 为函数 y x 2(a x b) 的图象,其中 (0 a b) ,当该图形满足
lx ly 1时,请直接写出 a 的取值范围.
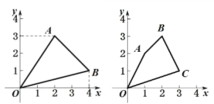
图 1 图 2
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图 1,六边形 ABCDEF 的每一个内角都相等.
(1)六边形 ABCDEF 每一个内角的度数是 ;
(2)在图 1 中,若 AF 2 ,AB 4 ,BC 3 ,CD 1 ,则 DE ,EF ;
(3)如图 2,在(2)的条件下,若 M 、N 分别为边 AF 、 AB 的中点,连接 CM 、DN交于点 G ,求![]() 的值.
的值.
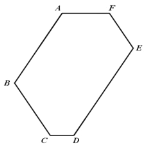
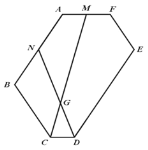
图 1 图 2
查看答案和解析>>
科目: 来源: 题型:
【题目】为活跃校园气氛,增强班集体凝聚力,培养学生团结协作的意识,我校计划在初一、初二举行学生趣味运动会.学校计划用不超过4620元购买足球和篮球共28个,分别作为运动会团体一、二等奖的奖品.已知足球单价180元,篮球单价160元.
(1)学校至多可购买多少个足球?
(2)为了鼓励更多班级参与运动,学校决定在计划经费内,按(1)问的结果购买足球作为一等奖奖品.购买奖品时正好赶上商场对商品价格进行调整,足球单价上涨了a%,篮球单价下降了![]() a%,最终恰好比计划经费的最大值节余了196元,求a的值.
a%,最终恰好比计划经费的最大值节余了196元,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在 RtABC 中,ACB 90,点O在 BC 上,经过点 的⊙ O 与 BC ,AB 分别相交于点 D ,E 连接 CE , CE CA .
(1)求证: CE 是⊙ O 的切线;
(2)若 tan ABC ![]() ,BD 4,求CD 的长.
,BD 4,求CD 的长.
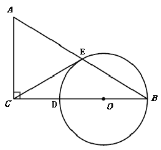
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上,请按要求画图和填空:
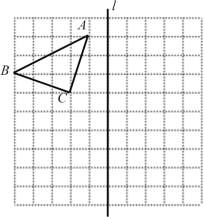
(1)在网格中画出△ABC向下平移5个单位得到的△A1B1C1;
(2)在网格中画出△A1B1C1关于直线l对称的△A2B2C2;
(3)在网格中画出将△ABC绕点A按逆时针方向旋转90度得到的△AB3C3;
(4)在图中探究并求得△ABC的面积= (直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com