
科目: 来源: 题型:
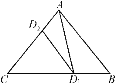
【题目】定义:若经过三角形顶点的一条直线把三角形分割出至少一个图形与原三角形相似,则称这条直线为三角形的自似线,如图,△ABC中,AC=b,BC=a,∠C<∠B<∠A,过顶点A作∠CAD1=∠B,交边BC于点D1,依次过顶点D1作∠CD1D2=∠CAD1,过点D2作∠CD2D3=∠CD1D2,…,过点Dn-1作∠CDn-1Dn=∠CDn-2Dn-1.
(1)试证直线AD1是△ABC的自似线;
(2)试求线段CD1的长,并猜想CDn的长;
(3)当60°<∠A<120°,且n=5时,与△ABC相似的三角形有几个?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
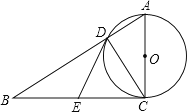
(1)求证:点E是边BC的中点;
(2)求证:BC2=BDBA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.
查看答案和解析>>
科目: 来源: 题型:
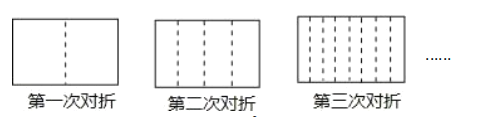
【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到![]() 条折痕,那么对折四次可以得到( )条折痕.如果对折
条折痕,那么对折四次可以得到( )条折痕.如果对折![]() 次, 可以得到( )条折痕
次, 可以得到( )条折痕
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图①,在△ABC中,∠BAC=90,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D. A.E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D. A.E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。

查看答案和解析>>
科目: 来源: 题型:
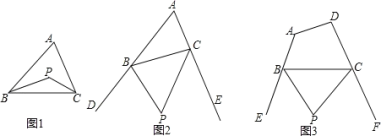
【题目】(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70,则∠BPC=_______度;
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由。
(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.,直接写出∠BPC与α的数量关系;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=a.
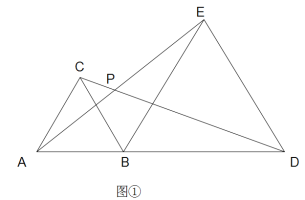
(1)当a=60°, 如图①则,∠DPE的度数______________
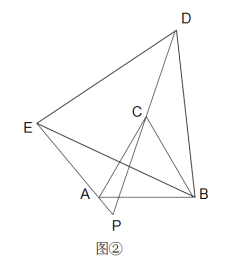
(2)若△BDE绕点B旋转一定角度,如图②所示,求∠DPE(用a表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,点![]() ,点
,点![]() 分别在
分别在![]() 轴正半轴和负半轴上,
轴正半轴和负半轴上,![]() .
.
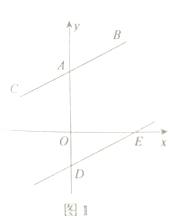
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)在![]() 和
和![]() 内作射线
内作射线![]() ,
,![]() ,分别与过
,分别与过![]() 点的直线交于第一象限内的点
点的直线交于第一象限内的点![]() 和第三象限内的点
和第三象限内的点![]() .
.
①如图2,若![]() ,
,![]() 恰好分别平分
恰好分别平分![]() 和
和![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,当
,当![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com