
科目: 来源: 题型:
【题目】阅读并回答问题.
求一元二次方程ax2+bx+c=0(a≠0)的根(用配方法).
解:ax2+bx+c=0,
∵a≠0,∴x2+![]() x+
x+![]() =0,第一步
=0,第一步
移项得:x2+![]() x=﹣
x=﹣![]() ,第二步
,第二步
两边同时加上(![]() )2,得x2+
)2,得x2+![]() x+(____)2=﹣
x+(____)2=﹣![]() +(
+(![]() )2,第三步
)2,第三步
整理得:(x+![]() )2=
)2=![]() 直接开方得x+
直接开方得x+![]() =±
=±![]() ,第四步
,第四步
∴x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ,第五步
,第五步
上述解题过程是否有错误?若有,说明在第几步,指明产生错误的原因,写出正确的过程;若没有,请说明上述解题过程所用的方法.
查看答案和解析>>
科目: 来源: 题型:
【题目】根的判别式内容:
△=b2﹣4ac>0一元二次方程_____;
△=b2﹣4ac=0一元二次方程_____;
此时方程的两个根为x1=x2=_____.
△=b2﹣4ac<0一元二次方程_____.
△=b2﹣4ac≥0一元二次方程_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AM∥BN,∠A=52°,点P是射线AM上的动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读并回答问题.
求一元二次方程ax2+bx+c=0(a≠0)的根(用配方法).
解:ax2+bx+c=0,
∵a≠0,∴x2+![]() x+
x+![]() =0,第一步
=0,第一步
移项得:x2+![]() x=﹣
x=﹣![]() ,第二步
,第二步
两边同时加上(![]() )2,得x2+
)2,得x2+![]() x+( )2=﹣
x+( )2=﹣![]() +(
+(![]() )2,第三步
)2,第三步
整理得:(x+![]() )2=
)2=![]() 直接开方得x+
直接开方得x+![]() =±
=±![]() ,第四步
,第四步
∴x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ,第五步
,第五步
上述解题过程是否有错误?若有,说明在第几步,指明产生错误的原因,写出正确的过程;若没有,请说明上述解题过程所用的方法.
查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读,再填空解题:
①方程x2﹣x﹣6=0的根是x1=3,x2=﹣2,则x1+x2=1,x1x2=﹣6;
②方程2x2﹣7x+3=0的根是x1=![]() ,x2=3,则x1+x2=
,x2=3,则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
根据以上①②你能否猜出:
如果关于x的一元二次方程ax2+bx+c=0(a≠0,且a、b、c为常数,b2﹣4ac≥0)有两根x1、x2,那么x1+x2、x1x2与系数a、b、c有什么关系?请写出你的猜想并说明理由.
利用公式法求出方程的根即可.
查看答案和解析>>
科目: 来源: 题型:
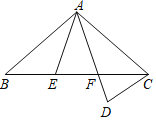
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程(m+1)x2+2mx+(m﹣3)=0有实数根.
(1)求m的取值范围;
(2)m为何值时,方程有两个相等的实数根?并求出这两个实数根.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点E,F分别在正方形ABCD的边BC,CD上.若AF平分∠DFE,∠AFE=55°,则∠AEB的度数为( )
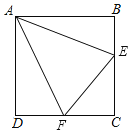
A.75°B.55°C.80°D.45°
查看答案和解析>>
科目: 来源: 题型:
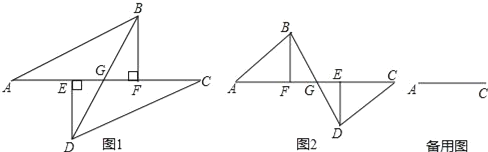
【题目】如图1所示,点E、F在线段AC上,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为点E,F;DE,BF分别在线段AC的两侧,且AE=CF,AB=CD,BD与AC相交于点G.
(1)求证:EG=GF;
(2)若点E在F的右边,如图2时,其余条件不变,上述结论是否成立?请说明理由.
(3)若点E、F分别在线段CA的延长线与反向延长线上,其余条件不变,(1)中结论是否成立?(要求:在备用图中画出图形,直接判断,不必说明理由)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com