练习册

  • 练习册
  • 试题
    相关习题
     0  357186  357194  357200  357204  357210  357212  357216  357222  357224  357230  357236  357240  357242  357246  357252  357254  357260  357264  357266  357270  357272  357276  357278  357280  357281  357282  357284  357285  357286  357288  357290  357294  357296  357300  357302  357306  357312  357314  357320  357324  357326  357330  357336  357342  357344  357350  357354  357356  357362  357366  357372  357380  366461 

    科目： 来源： 题型：

    【题目】如图，已知在Rt△ABC中，∠ACB=90°，AC=8，BC=16，D是AC上的一点，CD=3，点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连结AP.

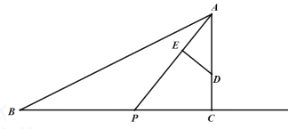
    （1）当t=3秒时，求AP的长度(结果保留根号)；

    （2）当△ABP为等腰三角形时，求t的值；

    （3）过点D做DE⊥AP于点E.在点P的运动过程中，当t为何值时，能使DE=CD？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】随着人们生活质量的提高，净水器已经慢慢走入了普通百姓家庭，某电器公司销售每台进价分别为 2000 元，1700 元的A，B两种型号的净水器，下表是近两周的销售情况：

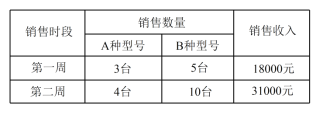
    （1）求A，B两种型号的净水器的销售单价；

    （2）若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台，求 A种型号的净水器最多能采购多少台?

    （3）在（2）的条件下，公司销售完这 30 台净水器能否实现利润超过12800 元的目标?若能，请给出相应的采购方案；若不能，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】BD、CE分别是△ABC的边AC、AB上的高，P在BD的延长线上，且BP=AC，点Q在CE上，CQ=AB,

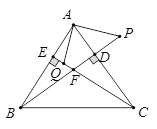
    求证：（1）AP=AQ ；

    （2）AP⊥AQ．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】请阅读下列材料：已知方程x2+x﹣3=0，求一个一元二次方程，使它的根分别是已知方程根的2倍．

    解：设所求方程的根为y，则y=2x．所以x=．

    把x=代入已知方程，得（）2+﹣3=0，化简，得y2+2y﹣12=0．

    故所求方程为y2+2y﹣12=0．

    这种利用方程根的代换求新方程的方法，我们称为“换根法”．

    问题：已知方程x2+x﹣1=0，求一个一元二次方程，使它的根分别是已知方程根的3倍．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知：如图，在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG⊥CE于G，且CD=AE.

    （1）求证：CG=EG.

    （2）求证：∠B=2∠ECB.

    查看答案和解析>>

    科目： 来源： 题型：

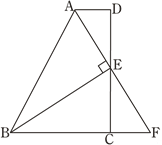
    【题目】如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F. 已知AD=2cm，BC=5cm.

    （1）求证：FC=AD；

    （2）求AB的长.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】为了解九年级学生的体能情况，学校组织了一次体能测试，并随机选取50名学生的成绩进行统计，得出相关统计表和统计图（其中部分数据不慎丢失，暂用字母m，n表示）．

    成绩等级

    优秀

    良好

    合格

    不合格

    人数

    m

    30

    n

    5

    请根据图表所提供的信息回答下列问题：

    （1）统计表中的m=　 　，n=　 　；并补全频数分布直方图；

    （2）若该校九年级有500名学生，请据此估计该校九年级学生体能良好以上的学生有多少人？

    （3）根据以往经验，经过一段时间训练后，有60%的学生成绩可以上升一个等级，请估计经过训练后九年级学生体能达标率（成绩在良好及以上）

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O，∠B的平分线BE交AC于D，交⊙O于E，过E作EF∥AC交BA的延长线于F．

    （1）求证：EF是⊙O切线；

    （2）若AB=15，EF=10，求AE的长．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，P是等边三角形ABC内一点，且PA=4，PB=，PC=2，以下五个结论：①∠ BPC=120°；②∠APC=120°；③；④AB=；⑤点P到△ABC三边的距离分别为PE,PF,PG,则有 其中正确的有（ ）

    A.4个B.3个C.2个D.1个

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】一位运动员在距篮下4m处跳起投篮，球运行的路线是抛物线，当球运行的水平距离是2.5m时，达到最大高度3.5m，然后准确落入篮圈．已知篮圈中心到地面的距离为3.05m．

    （1）建立如图所示的平面直角坐标系，求抛物线的解析式．

    （2）该运动员身高1.8m，在这次跳投中，球在头顶上0.25m处出手，

    问：球出手时，他距离地面的高度是多少？

    查看答案和解析>>

    同步练习册答案