
科目: 来源: 题型:
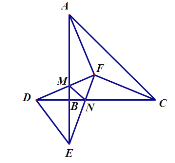
【题目】如图,直角三角形ABC与直角三角形BDE中,点B,C,D在同一条直线上,已知AC=AE=CD,∠BAC和∠ACB的角平分线交于点F,连DF,EF,分别交AB、BC于M、N,已知点F到△ABC三边距离为3,则△BMN的周长为____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,菱形ABCD的较短对角线BD为4,∠ADB=60°,E、F分别在AD,CD上,且∠EBF=60°.
(1)求证:△ABE≌△DBF;
(2)判断△BEF的形状,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是_____,B点表示的实际意义是_____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.

查看答案和解析>>
科目: 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,八年级1、2班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据统计图所给的信息填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | 85 | _____ | 85 |
八(2) | _____ | 80 | _____ |
(2)若八(1)班复赛成绩的方差s12=70,请计算八(2)班复赛成绩的方差s22,并说明哪个班级5名选手的复赛成绩更平稳一些.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着科技进步,无人机的应用越来越广,如图1,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部C的俯角.

(1)如果上述仰角与俯角分别为30°与60°,且该楼的高度为30米,求该时刻无人机的竖直高度CD;
(2)如图2,如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=3,BC=6.求平行四边形ABCD的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,分别在AB的右侧、AC的左侧作等边△ABE和等边△ACD,BE与CD相交于点F,连接BD,若BD=BF,则∠BDF为__________度.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=5,AC=![]() ,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短长为( )
,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AD垂直BC于点D,且AD=BC,BC上方有一动点P满足![]() ,则点P到B、C两点距离之和最小时,∠PBC的度数为( )
,则点P到B、C两点距离之和最小时,∠PBC的度数为( )

A.30°B.45°C.60°D.90°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:Rt△ABC中,∠C=90°,∠ABC=30°.

(1)探究应用1:如图1,Rt△ABC中,∠C=90°,∠ABC=30°,点D在线段CB上,以AD为边作等边△ADE,连接BE,为探究线段BE与DE之间的数量关系,组长已经添加了辅助线:取AB的中点F,连接EF.线段BE与DE之间的数量关系是_________,并说明理由;
(2)探究应用2:如图2,Rt△ABC中,∠C=90°,∠ABC=30°,点D在线段CB的延长线上,以AD为边作等边△ADE,连接BE.线段BE与DE之间的数量关系是__________,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com