科目： 来源： 题型：
【题目】如图，在△ABC中，∠BAC=90°，AB=AC．点D从点B出发沿射线BC移动，以AD为边在AB的右侧作△ADE，且∠DAE=90°，AD=AE．连接CE．
（1）如图1，若点D在BC边上，则∠BCE=______度；
（2）如图2，若点D在BC的延长线上运动．
①∠BCE的度数是否发生变化？请说明理由；
②若BC=6，CD=2，求△ADE的面积．
查看答案和解析>>
科目： 来源： 题型：
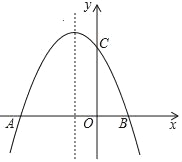
【题目】抛物线y=﹣x2+bx+c与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C．
（1）求该抛物线的解析式；
（2）在抛物线上求一点P，使S△PAB=S△ABC，写出P点的坐标；
（3）在抛物线的对称轴上是否存在点Q，使得△QBC的周长最小？若存在，求出点Q的坐标，若不存在，请说明理由．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，AB是⊙O的直径，M是OA上一点，过M作AB的垂线交AC于点N，交BC的延长线于点E，直线CF交EN于点F，若∠BAC=30°，且∠ECF=∠E．
（1）试判断CF与⊙O的位置关系，并说明理由；
（2）设⊙O的半径为2，且AC=CE，求AM的长．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在等边三角形ABC中，点D，E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．
（1）求∠F的度数；
（2）若CE=4，求DF的长．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，反比例函数y=
与一次函数y=kx+b的图象交于点A（﹣2，1），B（1，n），交y轴于点C．
（1）求反比例函数与一次函数的解析式；
（2）求△AOB的面积；
（3）若点P是y轴上的点，请直接写出能使△PAC为等腰三角形的点P的坐标．
查看答案和解析>>
科目： 来源： 题型：
【题目】基本事实:两角及其夹边分别相等的两个三角形全等(简称
).请你在此基础上解决下面问题:
(1)叙述三角形全等的判定方法中的
;
(2)证明.要求:叙述要用文字表达;用图形中的符号表达已知、求证,并证明，证明时各步骤要注明依据.
查看答案和解析>>
科目： 来源： 题型：
【题目】问题：如图①，在直角三角形
中，
，
于点
，可知
（不需要证明）；
（1）探究：如图②，
，射线
在这个角的内部，点
、
在
的边
、
上，且
，
于点
，
于点．证明：
；
（2）证明：如图③，点、在的边、上，点
、在内部的射线
上，
、
分别是
、
的外角。已知，
．求证：
；
（3）应用：如图④，在
中，，
．点在边
上，
，点、在线段上，．若的面积为15，则
与
的面积之和为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
