
科目: 来源: 题型:
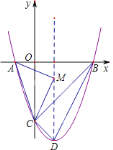
【题目】如图所示:抛物线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 、
、![]() 三点,
三点,![]() 是抛物线的顶点,
是抛物线的顶点,![]() 在对称轴上,
在对称轴上,![]() 在坐标轴上.以下结论:
在坐标轴上.以下结论:
①存在点![]() ,使
,使![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() 的最小值是
的最小值是![]() ;③
;③![]() 的最大值是
的最大值是![]() ;④若
;④若![]() 与
与![]() 相似,则
相似,则![]() 的坐标恰有两个.
的坐标恰有两个.
其中正确的是________(只填序号)
查看答案和解析>>
科目: 来源: 题型:
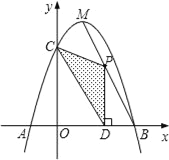
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题
数学课上,老师出示了这样一道题:如图,![]() 中,
中,![]() ,点P为边AB上一点(不与A、B重合),过P作
,点P为边AB上一点(不与A、B重合),过P作![]() 于Q,做QE∥AB交BC于点E,连接PE,将线段PE绕点P顺时针旋转90°到PF,连接QF,探究线段
于Q,做QE∥AB交BC于点E,连接PE,将线段PE绕点P顺时针旋转90°到PF,连接QF,探究线段![]() 之间的数量关系并证明.
之间的数量关系并证明.
同学们经过思考后,交流了自已的想法
小明:“通过观察和度量,发现![]() 为直角.”
为直角.”
小伟:“我通过一线三直角的模型构造三角形全等可以解决问题.”
小强:“我构造等腰直角三角形,再利用全等三角形可以解决问题.”
老师:“若其他条件不变,PE=![]() AC,就可以求出
AC,就可以求出![]() 的值.”
的值.”
(1)![]() 多少度?四边形
多少度?四边形![]() 为什么特殊四边形?(直接写出答案)
为什么特殊四边形?(直接写出答案)
(2)探究线段![]() 之间的数量关系并证明;
之间的数量关系并证明;
(3)若其他条件不变,PE=![]() AC,求
AC,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 、
、![]() 分别是边长
分别是边长![]() 为的等边
为的等边![]() 的边
的边![]() ,
,![]() 上的动点,点
上的动点,点![]() 从顶点
从顶点![]() ,点
,点![]() 从顶点
从顶点![]() 同时出发,分别沿
同时出发,分别沿![]() ,
,![]() 边运动,点
边运动,点![]() 到点
到点![]() 停止,点
停止,点![]() 到点
到点![]() 停止.社运动时间为
停止.社运动时间为![]() 秒,他们的速度都为
秒,他们的速度都为![]() .
.

(1)连接![]() ,
,![]() 相交于
相交于![]() ,在点
,在点![]() ,
,![]() 的运动过程中
的运动过程中![]() 的大小是否变化?若变化,说明理由;若不变,求出它的度数;
的大小是否变化?若变化,说明理由;若不变,求出它的度数;
(2)当![]() 取何值时,
取何值时,![]() 是直角三角形.
是直角三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰直角![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() 的外角平分线以及
的外角平分线以及![]() 的平分线交于点
的平分线交于点![]() ,(1)结论是否成立?请在图中补全图形,写出结论,并说明理由.
,(1)结论是否成立?请在图中补全图形,写出结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系中,OC OD,OC OD ,DC 的延长线交 y 轴正半轴上点 B ,过点C 作CA BD 交 x 轴负半轴于点A .

(1)如图1,求证:OAOB
(2)如图1,连AD,作OM ∥AC交AD于点M,求证: BC 2OM
(3)如图2,点E为OC 的延长线上一点,连DE,过点D作DFDE且DF DE ,连CF 交 DO 的延长线于点G 若OG 4,求CE 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校有一块长方形活动场地,长为![]() 米,宽比长少
米,宽比长少![]() 米,实施“阳光体育”行动以后,学校为了扩大学生的活动场地,让学生能更好地进行体育活动,将操场的长和宽都增加
米,实施“阳光体育”行动以后,学校为了扩大学生的活动场地,让学生能更好地进行体育活动,将操场的长和宽都增加![]() 米.
米.
(1)求活动场地原来的面积是多少平方米.(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,求活动场地面积增加后比原来多多少平方米.
,求活动场地面积增加后比原来多多少平方米.

查看答案和解析>>
科目: 来源: 题型:
【题目】“金山”超市现有甲、乙两种糖果若干kg,两种糖果的售价和进价如表
糖果 | 甲种 | 乙种 |
售价 | 36元/kg | 20元/kg |
进价 | 30元/kg | 16元/kg |
(1)超市准备用甲、乙两种糖果混合成杂拌糖出售,混合后糖果的售价是27.2元/kg,现要配制这种杂拌糖果100/kg,需要甲、乙两种糖果各多少千克?
(2)“六一”儿童节前夕,超市准备用5000元购进甲、乙两种糖果共200kg,如何进货才能使这批糖果获得最大利润,最大利润是多少?(注:进货量只能为整数)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,CE⊥AB,BD⊥AC,垂足分别为E、D,BD、CE交于点O,AB=AC,∠B=20°,则∠AOD=( )

A. 20°B. 40°C. 50°D. 55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com