A. 4 B. 8 C. 10 D. 12

【题目】解方程：（1）；（2）；（3）+1=．

【题目】如图，在四边形ABCD中，AB=AD，对角线AC，BD交于点E，点O在线段AE上，⊙O过B，D两点，若OC=5，OB=3，且cos∠BOE=．求证：CB是⊙O的切线．

(1)按上面材料提示的方法填空：a2﹣4a＝　 　＝　 　．﹣a2+12a＝　 　＝　 　．

(2)探究：当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值？请说明理由．

(3)应用：如图．已知线段AB＝6，M是AB上的一个动点，设AM＝x，以AM为一边作正方形AMND，再以MB、MN为一组邻边作长方形MBCN．问：当点M在AB上运动时，长方形MBCN的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．

【题目】一般情况下，不成立，但有些数可以使得它成立，例如：a＝1，b＝2．我们称使得成立的一对数a，b为“相伴数对”，记为（a，b）．

（1）判断数对（﹣2，1），（3，3）是否是“相伴数对”；

（2）若（k，﹣1）是“相伴数对”，求k的值；

（3）若（4，m）是“相伴数对”，求代数式的值．

解方程

解：整理，得： …………………………第①步

去分母，得： …………………………第②步

移项，得： ……………………… 第③步

合并同类项，得： ……………………… 第④步

系数化1，得： …………………………第⑤步

检验：当时，

所以原方程的解是． ………………………第⑥步

上述晶晶的解题过程从第_____步开始出现错误，错误的原因是_________________．请你帮晶晶改正错误，写出完整的解题过程．

【题目】对于一元二次方程,下列说法:①若a+c=0,方程有两个不等的实数根;②若方程有两个不等的实数根,则方程也一定有两个不等的实数根;③若c是方程的一个根,则一定有成立;④若m是方程的一个根,则一定有成立.其中正确地只有 （ ）

A. ①② B. ②③ C. ③④ D. ①④

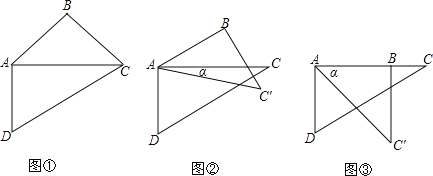
①当α为多少度时，AB∥DC？

②当旋转到图③所示位置时，α为多少度？

③连接BD，当0°＜α≤45°时，探求∠DBC′+∠CAC′+∠BDC值的大小变化情况，并给出你的证明．

解：设x2﹣4x＝y，

原式＝（y+2）（y+6）+4　（第一步）

＝y2+8y+16　（第二步）

＝（y+4）2（第三步）

＝（x2﹣4x+4）2（第四步）

（1）该同学第二步到第三步运用了因式分解的　 　（填序号）．

A．提取公因式 B．平方差公式

C．两数和的完全平方公式 D．两数差的完全平方公式

（2）该同学在第四步将y用所设中的x的代数式代换，得到因式分解的最后结果．这个结果是否分解到最后？　 　．（填“是”或“否”）如果否，直接写出最后的结果　 　．

（3）请你模仿以上方法尝试对多项式（x2﹣2x）（x2﹣2x+2）+1进行因式分解．

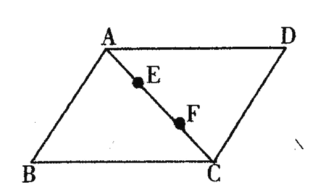
（1）连接 ；

（2）结论： = ；

（3）证明：