
科目: 来源: 题型:
【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,因为
是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,因为![]() ,所以可用、
,所以可用、![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是__________,小数部分是__________.
的整数部分是__________,小数部分是__________.
(2)如果![]() 的整数部分为
的整数部分为![]() ,小数部分为
,小数部分为![]() ,求
,求![]() 的值.
的值.
(3)已知![]() ,其中
,其中![]() 是整数,且
是整数,且![]() .则求
.则求![]() 的平方根的值.
的平方根的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是____________________________________。
(2)三角形的“二分线”可以是__________________________________。
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.
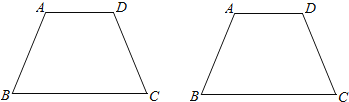
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目: 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目: 来源: 题型:
【题目】作出函数![]() 的图象,并利用图象回答问题:
的图象,并利用图象回答问题:
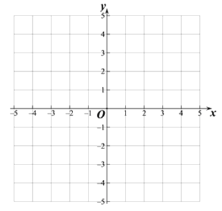
(1)写出图象与![]() 轴的交点A的坐标________,与
轴的交点A的坐标________,与![]() 轴的交点B的坐标________.
轴的交点B的坐标________.
(2)当![]() 时,
时,![]() 的取值范围是______________.
的取值范围是______________.
(3)有一点C的坐标是(3,4),顺次连接点A、B、C得到△ABC,三角形ABC的面积为________.
(4)点C关于![]() 轴对称的点D的坐标
轴对称的点D的坐标
(5)连接B,D两点,求直线BD的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】勾股定理在平面几何中有着不可替代的重要地位,在我国古算书(周髀算经》中就有“若勾三,股四,则弦五”的记载,如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理,将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( )
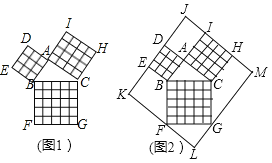
A.120B.110C.100D.90
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等边三角形ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边三角形CDE,连接BE
(1)若点D在线段AM上时,求证:△ADC≌△BEC;
(2)当动点D在直线AM上时,设直线BE与直线AM的交点为O,
①当动点D在线段AM的延长线上时,求当∠ACE为多少度时,点B、D、E在一条直线上;②当动点D在直线AM上时,试判断∠AOB是否为定值?并说明理由.
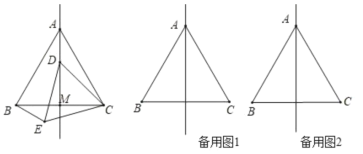
查看答案和解析>>
科目: 来源: 题型:
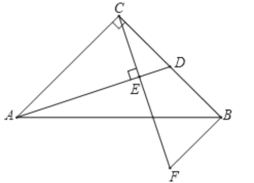
【题目】如图所示,在△ABC中,∠ACB=90°,AC=BC,D为BC边上的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F.
(1)求证:AC=2BF
(2)连接DF,求证:AB垂直平分DF
(3)连接AF,试判断△ACF的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的文字,解答问题:
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:如果
的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:如果![]() ,其中x是整数且0<y<1,那么x=1,y=
,其中x是整数且0<y<1,那么x=1,y=![]() .请解答:
.请解答:
(1)如果![]() =a+b,其中a是整数,且0<b<1,那么a= b= .
=a+b,其中a是整数,且0<b<1,那么a= b= .
(2)如果90+![]() =x+y,其中x是整数,且0<y<1,求x+
=x+y,其中x是整数,且0<y<1,求x+![]() +59-y的平方根.
+59-y的平方根.
(3)如果6+![]() 的整数部分为m,6-
的整数部分为m,6-![]() 的小数部分为n,求m-n-
的小数部分为n,求m-n-![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=![]() BC;④S△ACE=
BC;④S△ACE=![]() SABCD.其中正确的个数是( )
SABCD.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com