方案一：让每天所有取奶的人到奶站的距离总和最小；

方案二：让每天A楼与C楼所有取奶的人到奶站的距离之和等于B楼所有取奶的人到奶站的距离之和．

(1)若按照方案一建站，取奶站应建在什么位置?

(2)若按照方案二建站，取奶站应建在什么位置?

（1）求证：CF∥AB．

（2）求∠DFC的度数．

（1）求∠ADC的度数；

（2）求弦BD的长.

(1)求直线y＝kx＋b的解析式；

(2)求两条直线与y轴围成的三角形面积；

(3)直接写出不等式(k＋2)x＋b≥0的解集．

(1)请你计算这两组数据的平均数、中位数；

(2)现要从中选派一人参加操作技能比赛，从统计学的角度考虑，你认为选派哪名工人参加合适？请说明理由．

A. B.

C. D.

(1)求图象的开口方向、对称轴、顶点坐标；

(2)求图象与x轴的交点坐标，与y轴的交点坐标；

(3)当x为何值时，y随x的增大而增大？

重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为( )

A. 3 B. 4

C. 5 D. 6

【题目】如图①，、两个圆柱形容器放置在同一水平桌面上，开始时容器中盛满水，容器中盛有高度为1 dm的水，容器下方装有一只水龙头，容器向容器匀速注水.设时间为t (s)，容器、中的水位高度(dm)、(dm)与时间t (s)之间的部分函数图像如图②所示.根据图中数据解答下列问题:

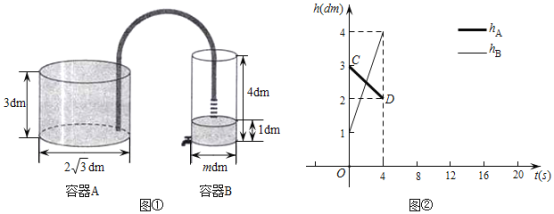
(1)容器向容器注水的速度为 dm3/s(结果保留)，容器的底面直径 dm;

(2)当容器注满水后，容器停止向容器注水，同时开启容器的水龙头进行放水，放水速度为dm3/s.请在图②中画出容器中水位高度与时间 ()的函数图像，说明理由;

(3)当容器B注满水后，容器A继向容器B注水，同时开启容器B的水龙头进行放水，放水速度为dm3/s，直至容器、水位高度相同时，立即停止放水和注水，求容器向容器全程注水时间.(提示:圆柱体积=圆柱的底面积×圆柱的高)

【题目】如图，在边长为12cm的正方形中，是边的中点，点从点出发，在正方形边上沿的方向以大于1 cm/s的速度匀速移动，点从点出发，在边上沿方向以1 cm/s的速度匀速移动，、两点同时出发，当点、相遇时即停止移动.设点移动的时间为t(s)，正方形与的内部重叠部分面积为(cm2).已知点移动到点处，的值为96(即此时正方形与的内部重叠部分面积为96cm2).

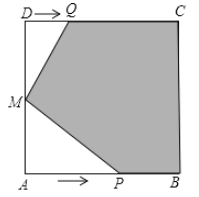
(1)求点的速度:

(2)求与t的函数关系式，并直接写出的取值范围.