
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,4),则点B4的坐标为_____,点B2017的坐标为_____.
,0),B(0,4),则点B4的坐标为_____,点B2017的坐标为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则sinB=![]() ,sinC=
,sinC=![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有:![]() ,
,![]() ,所以
,所以![]() .
.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目: 来源: 题型:
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | |
A村(元/辆) | B村(元/辆) | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是边长为8等边三角形,如图所示,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度,当点M第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,可得到等边三角形![]() ?
?
(2)点M、N运动几秒后,M、N两点重合?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰![]() ?如存在,请求出此时M、N运动的时间.
?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )

A.4 B.3 C.2 D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴x轴交于点D,点E(4,n)在抛物线上.
(1)求直线AE的解析式;
(2)连接CB,点K是线段CB的中点,点M是y轴上的一点,点P为直线CE下方抛物线上的一点,连接PC,PE,当△PCE的面积最大时,求KM+PM的最小值;
(3)点G是线段CE的中点,将抛物线y=x2﹣2x﹣3沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F,在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
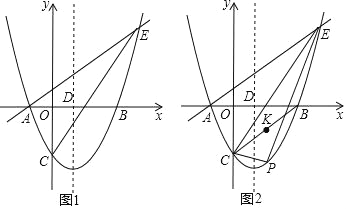
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年11月份,我县教体局由县城老区搬到了新区(海丰16路与棣新4路交叉口),当时某科室需要把相关档案由老区办公楼搬到新区办公楼,甲搬家公司单独工作了3天,完成总量的![]() ;这时为了加快进度,又调来乙搬家公司合干,两队又共同工作了3天,全部搬完档案。假若在工作期间甲、乙两搬家公司各自的工作效率不变,问若单独干完这项工作哪个搬家公司的速度快?(用方程解答)
;这时为了加快进度,又调来乙搬家公司合干,两队又共同工作了3天,全部搬完档案。假若在工作期间甲、乙两搬家公司各自的工作效率不变,问若单独干完这项工作哪个搬家公司的速度快?(用方程解答)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c与y轴的交于点A(0,3),与x轴的交于点B和C,点B的横坐标为2.点A关于抛物线对称轴对称的点为点D,在x轴上有一动点E(t,0),过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q.
x2+bx+c与y轴的交于点A(0,3),与x轴的交于点B和C,点B的横坐标为2.点A关于抛物线对称轴对称的点为点D,在x轴上有一动点E(t,0),过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当点P在线段AC的下方时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似.若存在,求出此时t的值;若不存在,请说明理由.
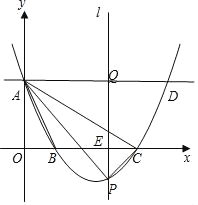
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于点C,该抛物线的顶点为M.
(1)求点A、B、C的坐标.
(2)求直线BM的函数解析式.
(3)试说明:∠CBM+∠CMB=90°.
(4)在抛物线上是否存在点P,使直线CP把△BCM分成面积相等的两部分?若存在,请求出点P的坐标;若不存在,请说明理由.
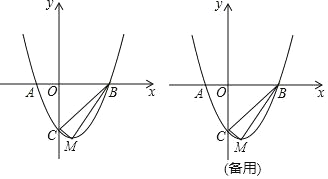
查看答案和解析>>
科目: 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间的函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com