
科目: 来源: 题型:
【题目】若一个矩形的短边与长边的比值为![]() (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.
![]() 操作:请你在如图所示的黄金矩形
操作:请你在如图所示的黄金矩形![]() 中,以短边
中,以短边![]() 为一边作正方形
为一边作正方形![]() ;
;
![]() 探究:在
探究:在![]() 中的四边形
中的四边形![]() 是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
是不是黄金矩形?若是,请予以证明;若不是,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】某文具店计划购进![]() ,
,![]() 两种笔记本共60本,每本
两种笔记本共60本,每本![]() 种笔记本比
种笔记本比![]() 种笔记本的利润高3元,销售2本
种笔记本的利润高3元,销售2本![]() 种笔记本与3本
种笔记本与3本![]() 种笔记本所得利润相同,其中
种笔记本所得利润相同,其中![]() 种笔记本的进货量不超过进货总量的
种笔记本的进货量不超过进货总量的![]() ,
,![]() 种笔记本的进货量不少于30本.
种笔记本的进货量不少于30本.
(1)每本![]() 种笔记本与
种笔记本与![]() 种笔记本的利润各为多少元?
种笔记本的利润各为多少元?
(2)设购进![]() 种笔记本
种笔记本![]() 本,销售总利润为
本,销售总利润为![]() 元,文具店应如何安排进货才能使得
元,文具店应如何安排进货才能使得![]() 最大?
最大?
(3)实际进货时,![]() 种笔记本进价下降
种笔记本进价下降![]() (
(![]() )元.若两种笔记本售价不变,请设计出笔记本销售总利润最大的进货方案.
)元.若两种笔记本售价不变,请设计出笔记本销售总利润最大的进货方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
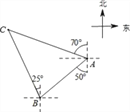
A. 10![]() 海里 B. 10
海里 B. 10![]() 海里 C. 10
海里 C. 10![]() 海里 D. 20
海里 D. 20![]() 海里
海里
查看答案和解析>>
科目: 来源: 题型:
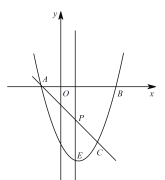
【题目】如图,抛物线y=ax2+bx-3与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点左侧),A(-1,0),B(3,0),直线
点左侧),A(-1,0),B(3,0),直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,其中
两点,其中![]() 点的横坐标为
点的横坐标为![]() 。
。
(1)求抛物线的函数解析式;
(2)![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 点作
点作![]() 轴的平行线交抛物线于
轴的平行线交抛物线于![]() 点,求线段
点,求线段![]() 长度的最大值;
长度的最大值;
(3)点![]() 是抛物线上的动点,在
是抛物线上的动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的
这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的![]() 点坐标;如果不存在,请说明理由。
点坐标;如果不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
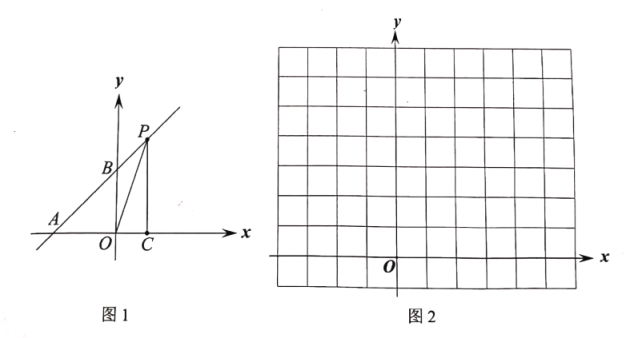
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 从
从![]() 点出发,沿射线
点出发,沿射线![]() 的方向运动,已知
的方向运动,已知![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,
,![]() ,记
,记![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式及
的函数关系式及![]() 的取值范围;
的取值范围;
(2)在图2所示的平面直角坐标系中画出(1)中所得函数的图象,记其与![]() 轴的交点为
轴的交点为![]() ,将该图象绕点
,将该图象绕点![]() 逆时针旋转
逆时针旋转![]() ,画出旋转后的图象;
,画出旋转后的图象;
(3)结合函数图象,直接写出旋转前后的图象与直线![]() 的交点坐标.
的交点坐标.
查看答案和解析>>
科目: 来源: 题型:
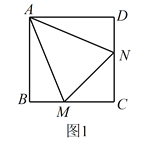
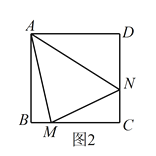
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() ,
,![]() (或它们的延长线)于点
(或它们的延长线)于点![]() ,
,![]() 。当
。当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .(不必证明)
.(不必证明)
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),线段
时(如图2),线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明。
之间有怎样的数量关系?写出猜想,并加以证明。
(2)当![]() 绕点
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() ,
,![]() 和
和![]() 之间又有怎样的数量关系?写出猜想,并加以证明。
之间又有怎样的数量关系?写出猜想,并加以证明。
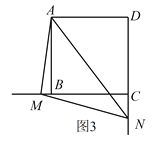
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com