
科目: 来源: 题型:
【题目】如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)这个云梯的底端B离墙多远?
(2)如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?

查看答案和解析>>
科目: 来源: 题型:
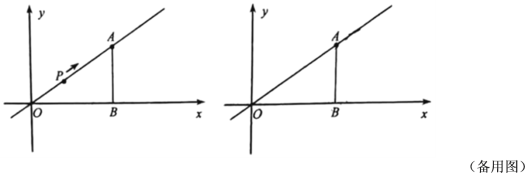
【题目】如图,已知![]() 为正比例函数
为正比例函数![]() 的图像上一点,
的图像上一点,![]() 轴,垂足为点
轴,垂足为点![]() .
.
(1)求![]() 的值;
的值;
(2)点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位的速度,沿射线
个单位的速度,沿射线![]() 方向运动.设运动时间为
方向运动.设运动时间为![]()
![]() .
.
①过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
②在点![]() 的运动过程中,是否存在这样的
的运动过程中,是否存在这样的![]() ,使得
,使得![]() 为等腰三角形?若存在,请求出所有符合题意的
为等腰三角形?若存在,请求出所有符合题意的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】勾股定理是数学史上非常重要的一个定理.早在![]() 多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以
多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以![]() 的三边为边长,向外作正方形
的三边为边长,向外作正方形![]() 、
、![]() 、
、![]() .
.
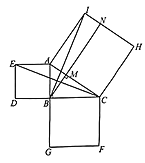
(1)连接![]() 、
、![]() ,求证:
,求证:![]()
(2)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
①试说明四边形![]() 与正方形
与正方形![]() 的面积相等;
的面积相等;
②请直接写出图中与正方形![]() 的面积相等的四边形.
的面积相等的四边形.
(3)由第(2)题可得:正方形![]() 的面积
的面积![]() 正方形
正方形![]() 的面积
的面积![]() _______________的面积,即在
_______________的面积,即在![]() 中,
中,![]() __________________.
__________________.
查看答案和解析>>
科目: 来源: 题型:
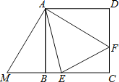
【题目】如图,四边形是正方形,![]() ,
,![]() 垂直
垂直![]() ,点
,点![]() 、
、![]() 、
、![]() 在一条直线上,且
在一条直线上,且![]() 与
与![]() 恰好关于所在直线成轴对称.已知
恰好关于所在直线成轴对称.已知![]() ,正方形边长为
,正方形边长为![]() .
.
![]() 图中
图中![]() 可以绕点________按________时针方向旋转________后能够与
可以绕点________按________时针方向旋转________后能够与![]() ________重合;
________重合;
![]() 写出图中所有形状、大小都相等的三角形________;
写出图中所有形状、大小都相等的三角形________;
![]() 用
用![]() 、
、![]() 的代数式表示
的代数式表示![]() 与
与![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图l、图2和图3所示(阴影部分为草坪).

请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图l,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果生产基地销售苹果,提供两种购买方式供客户选择
方式![]() :若客户缴纳
:若客户缴纳![]() 元会费加盟为生产基地合作单位,则苹果成交价为
元会费加盟为生产基地合作单位,则苹果成交价为![]() 元
元![]() 千克.
千克.
方式![]() :若客户购买数量达到或超过
:若客户购买数量达到或超过![]() 千克,则成交价为
千克,则成交价为![]() 元
元![]() 千克;若客户购买数量不足
千克;若客户购买数量不足![]() 千克,则成交价为
千克,则成交价为![]() 元
元![]() 千克.设客户购买苹果数量为
千克.设客户购买苹果数量为![]() (千克),所需费用为
(千克),所需费用为![]() (元).
(元).
(1)若客户按方式![]() 购买,请写出
购买,请写出![]() (元)与
(元)与![]() (千克)之间的函数表达式;(备注:按方式购买苹果所需费用
(千克)之间的函数表达式;(备注:按方式购买苹果所需费用![]() 生产基地合作单位会费
生产基地合作单位会费![]() 苹果成交总价)
苹果成交总价)
(2)如果购买数量超过![]() 千克,请说明客户选择哪种购买方式更省钱;
千克,请说明客户选择哪种购买方式更省钱;
(3)若客户甲采用方式![]() 购买,客户乙采用方式
购买,客户乙采用方式![]() 购买,甲、乙共购买苹果
购买,甲、乙共购买苹果![]() 千克,总费用共计
千克,总费用共计![]() 元,则客户甲购买了多少千克苹果?
元,则客户甲购买了多少千克苹果?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com