练习册

  • 练习册
  • 试题
    相关习题
     0  359671  359679  359685  359689  359695  359697  359701  359707  359709  359715  359721  359725  359727  359731  359737  359739  359745  359749  359751  359755  359757  359761  359763  359765  359766  359767  359769  359770  359771  359773  359775  359779  359781  359785  359787  359791  359797  359799  359805  359809  359811  359815  359821  359827  359829  359835  359839  359841  359847  359851  359857  359865  366461 

    科目： 来源： 题型：

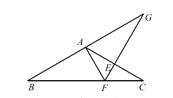
    【题目】如图，在△ABC 中，AB＝AC，∠BAC＝120°，AC 的垂直平分线交 BC 于 F，交 AC 于 E，交 BA 的延长线于 G，若 EG＝3，则 BF 的长是______．

    查看答案和解析>>

    科目： 来源： 题型：

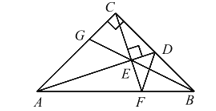
    【题目】如图：Rt△ABC 中，AC＝BC，∠ACB＝90°，D 为 BC 边中点，CF⊥AD 交 AD 于 E，交 AB 于 F，BE交 AC 于 G，连 DF，下列结论：①AC＝AF，②CD＋DF＝AD，③∠ADC＝∠BDF，④CE＝BE，⑤∠ BED＝45°，其中正确的有（ ）

    A. 5 个B. 4 个C. 3 个D. 2 个

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】关于x的方程,

    (1)a为何值时,方程的一根为0?

    (2)a为何值时,两根互为相反数?

    (3)试证明：无论a取何值,方程的两根不可能互为倒数．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】△ABC 中，AB＝AC，过其中一个顶点的直线可以把这个三角形分成另外两个等腰三角形，则∠BAC（ ）

    A. 36°，90°，， 108°B. 36°，72°，，90°

    C. 90°，72°，108°，D. 36°，90°，108°，

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知一抛物线与x轴的交点是A（﹣2，0），B（1，0），且经过点C（2，8）．

    （1）求该抛物线的解析式，并写出顶点坐标．

    （2）直接写出当y＞8时，x的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

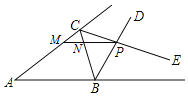
    【题目】如图△ABC 的∠ABC 的外角平分线 BD 与∠ACB 的外角平分线 CE 交于 P，过 P 作 MN∥AB 交 AC 于M，交 BC 于 N，且 AM＝8，BN＝5，则 MN＝（ ）

    A. 2B. 3C. 4D. 5

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知二次函数的图象如图所示，现有下列结论：①；②；③；④．则其中结论正确的是（ ）

    A. ①③ B. ③④ C. ②③ D. ①④

    查看答案和解析>>

    科目： 来源： 题型：

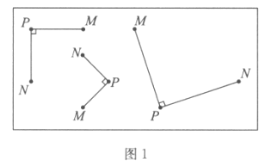
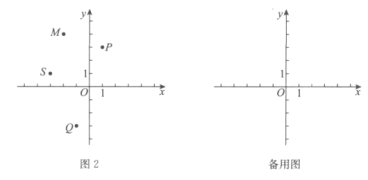
    【题目】如图1中的三种情况所示，对于平面内的点M，点N，点P，如果将线段PM绕点P顺时针旋转90°能得到线段PN，就称点N是点M关于点P的“正矩点”．

    （1）在如图2所示的平面直角坐标系中，已知，．

    ①在点P，点Q中，___________是点S关于原点O的“正矩点”；

    ②在S，P，Q，M这四点中选择合适的三点，使得这三点满足：

    点_________是点___________关于点___________的“正矩点”，写出一种情况即可；

    （2）在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B，点A关于点B的“正矩点”记为点C，坐标为．

    ①当点A在x轴的正半轴上且OA小于3时，求点C的横坐标的值；

    ②若点C的纵坐标满足，直接写出相应的k的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

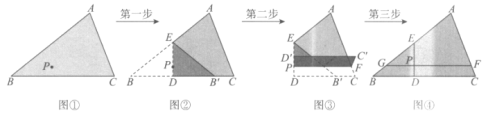
    【题目】已知：如图①所示的三角形纸片内部有一点P．

    任务：借助折纸在纸片上画出过点P与BC边平行的线段FG．

    阅读操作步骤并填空：

    小谢按图①～图④所示步骤进行折纸操作完成了画图任务．

    在小谢的折叠操作过程中，

    （1）第一步得到图②，方法是：过点P折叠纸片，使得点B落在BC边上，落点记为，折痕分别交原AB，BC边于点E，D，此时∠即∠=__________°；

    （2）第二步得到图③，参考第一步中横线上的叙述，第二步的操作指令可叙述为：_____________，并求∠EPF的度数；

    （3）第三步展平纸片并画出两次折痕所在的线段ED，FG得到图④．

    完成操作中的说理：

    请结合以上信息证明FG∥BC．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图1，在等腰直角三角形中，,点在边上，连接，连接

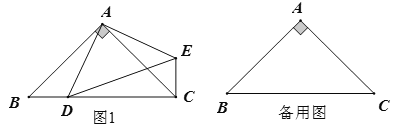
    （1）求证：

    （2）点关于直线的对称点为，连接

    ①补全图形并证明

    ②利用备用图进行画图、试验、探究，找出当三点恰好共线时点的位置，请直接写出此时的度数，并画出相应的图形

    查看答案和解析>>

    同步练习册答案