
科目: 来源: 题型:
【题目】已知关于![]() 的一元二次方程x2-(k+2)x+k-1=0
的一元二次方程x2-(k+2)x+k-1=0
(1)若方程的一个根为 -1,求![]() 的值和方程的另一个根;
的值和方程的另一个根;
(2)求证:不论![]() 取何值,该方程都有两个不相等的实数根.
取何值,该方程都有两个不相等的实数根.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划在规定时间内生产5G手机24000部,若每天比原计划多生产30部,则在规定时间内可以多生产300部.
(1)求原计划每天生产手机多少部?规定的天数是多少天?
(2)为了提前完成生产任务,公司在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线同时进行生产,已知每组机器人生产流水线每天生产手机的部数与20个工人原计划每天生产的手机总数相同,按此测算,恰好提前两天完成24000部5G手机的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是![]() 的网格图,请根据要求在网格中完成如下任务:
的网格图,请根据要求在网格中完成如下任务:
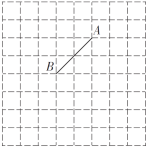
(1)请在网格中建立平面直角坐标系,使点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;(要求:画出
;(要求:画出![]() 轴、
轴、![]() 轴,并标出
轴,并标出![]() 、
、![]() 和原点
和原点![]() )
)
(2)以![]() 为一边,在网格中作等腰直角三角形
为一边,在网格中作等腰直角三角形![]() ,找出所有符合条件的
,找出所有符合条件的![]() 点,用
点,用![]() 、
、![]() ……表示,并写出它们的坐标.
……表示,并写出它们的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个长方形的周长是24厘米,它的一边长是![]() (单位:厘米),面积是
(单位:厘米),面积是![]() (单位:平方厘米).
(单位:平方厘米).
(1)若![]() ,则这个长方形的面积是__________平方厘米;
,则这个长方形的面积是__________平方厘米;
(2)写出![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)画出![]() 关于
关于![]() 的函数图象.
的函数图象.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(![]() 表示时间,
表示时间,![]() 、
、![]() 表示路程),根据图象解答下列问题:
表示路程),根据图象解答下列问题:
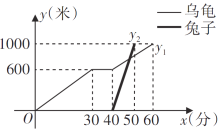
(1)“龟兔再次赛跑”的路程为__________米;
(2)它们两个约定__________先出发(填“兔子”和“乌龟”),先出发__________分钟;
(3)乌龟跑完全程用了__________分钟,兔子跑完全程用了__________分钟,乌龟平均速度是__________米/分,兔子平均速度是__________米/分;
(4)观察图象,你还能得出什么结论?
查看答案和解析>>
科目: 来源: 题型:
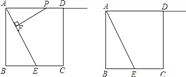
【题目】如图,正方形 ABCD 的边长为 4,E 是 BC 的中点,点 P 在射线 AD 上,过点 P 作 PF⊥AE,垂足为 F.
(1)求证:△PFA∽△ABE;
(2)当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶点的三角形也与△ABE
相似?若存在,求出 x 的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=3x与双曲线y=![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】
已知:如图(1),在平面直角坐标系中,点![]() ,
,![]() ,
,![]() 分别在坐标轴上,且
分别在坐标轴上,且![]() ,
,![]() 的面积为
的面积为![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 轴负方向以
轴负方向以![]() 个单位长度/秒的速度向下运动,连接
个单位长度/秒的速度向下运动,连接![]() ,
,![]() ,点
,点![]() 为
为![]() 上的中点.
上的中点.
(1)直接写出坐标![]() ___________,
___________,![]() ___________,
___________,![]() ___________.
___________.
(2)设点![]() 运动的时间为
运动的时间为![]() 秒,问:当
秒,问:当![]() 与
与![]() 垂直且相等时,求此时
垂直且相等时,求此时![]() 的值?并说明理由.
的值?并说明理由.
(3)如图(2)![]() ,在第四象限内有一动点
,在第四象限内有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,点
,点![]() 在第四象限内运动,当
在第四象限内运动,当![]() ,判断
,判断![]() 是否平分
是否平分![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com