
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD=![]() BC,等边△BEF的顶点F在BC上,边EF交AD于点P,若BE=10,BC=14,则PE的长为( )
BC,等边△BEF的顶点F在BC上,边EF交AD于点P,若BE=10,BC=14,则PE的长为( )

A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,正方形![]() 中,点
中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 在第一象限.动点
在第一象限.动点![]() 在正方形
在正方形![]() 的边上,从点
的边上,从点![]() 出发沿
出发沿![]() 匀速运动,同时动点
匀速运动,同时动点![]() 以相同速度在
以相同速度在![]() 轴上运动,当点
轴上运动,当点![]() 运动到点
运动到点![]() 时,两点同时停止运动,设运动时间为
时,两点同时停止运动,设运动时间为![]() 秒.当点
秒.当点![]() 在边
在边![]() 上运动时,点
上运动时,点![]() 的横坐标
的横坐标![]() (单位长度)关于运动时间
(单位长度)关于运动时间![]() (秒)的函数图象如图2所示.
(秒)的函数图象如图2所示.
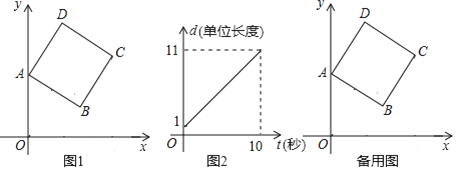
(1)正方形边长![]() _____________,正方形顶点
_____________,正方形顶点![]() 的坐标为__________________;
的坐标为__________________;
(2)点![]() 开始运动时的坐标为__________,点
开始运动时的坐标为__________,点![]() 的运动速度为_________单位长度/秒;
的运动速度为_________单位长度/秒;
(3)当点![]() 运动时,点
运动时,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)当点![]() 运动时,过点
运动时,过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴,垂足分别为点
轴,垂足分别为点![]() 、
、![]() ,且点
,且点![]() 位于点
位于点![]() 下方,
下方,![]() 与
与![]() 能否相似,若能,请直接写出所有符合条件的
能否相似,若能,请直接写出所有符合条件的![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境:在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,以
的中点,以![]() 为角的顶点作
为角的顶点作![]() .
.
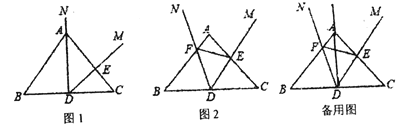
感知易证:(1)如图1,当射线![]() 经过点
经过点![]() 时,
时,![]() 交边
交边![]() 于点
于点![]() .将
.将![]() 从图1中的位置开始,绕点
从图1中的位置开始,绕点![]() 按逆时针方向旋转,使射线
按逆时针方向旋转,使射线![]() 、
、![]() 始终分别交边
始终分别交边![]() ,
,![]() 于点
于点![]() 、
、![]() ,如图2所示,易证
,如图2所示,易证![]() ,则有
,则有![]() .
.
操作探究:(2)如图2,![]() 与
与![]() 是否相似,若相似,请证明;若不相似,请说明理由;
是否相似,若相似,请证明;若不相似,请说明理由;
拓展应用:(3)若![]() ,直接写出当(2)中的旋转角为多少度时,
,直接写出当(2)中的旋转角为多少度时,![]() 与
与![]() 相似.
相似.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
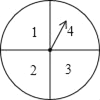
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018长春国际马拉松赛于2018年5月27日在长春市举行,其中10公里跑起点是长春体育中心,终点是卫星广场.比赛当天赛道上距离起点5km处设置一个饮料站,距离起点7.5km处设置一个食品补给站.小明报名参加了10公里跑项目.为了更好的完成比赛,小明在比赛前进行了一次模拟跑,从起点出发,沿赛道跑向终点,小明匀速跑完前半程后,将速度提高了![]() ,继续匀速跑完后半程.小明与终点之间的路程
,继续匀速跑完后半程.小明与终点之间的路程![]() 与时间
与时间![]() 之间的函数图象如图所示,根据图中信息,完成以下问题.(1公里=1千米)
之间的函数图象如图所示,根据图中信息,完成以下问题.(1公里=1千米)
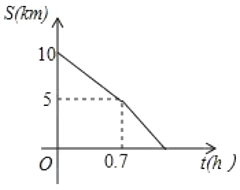
(1)小明从起点匀速跑到饮料站的速度为_______![]() ,小明跑完全程所用时间为________
,小明跑完全程所用时间为________![]() ;
;
(2)求小明从饮料站跑到终点的过程中![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求小明从起点跑到食品补给站所用时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司经营甲、乙两种商品,两种商品的进价和售价情况如下表:
进价(万元/件) | 售价(万元/件) | |
甲 | 12 | 14.5 |
乙 | 8 | 10 |
两种商品的进价和售价始终保持不变.现准备购进甲、乙两种商品共20件.设购进甲种商品![]() 件,两种商品全部售出可获得利润为
件,两种商品全部售出可获得利润为![]() 万元.
万元.
(1)![]() 与
与![]() 的函数关系式为__________________;
的函数关系式为__________________;
(2)若购进两种商品所用的资金不多于200万元,则该公司最多购进多少合甲种商品?
(3)在(2)的条件下,请你帮该公司设计一种进货方案,使得该公司获得最大利润,并求出最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目: 来源: 题型:
【题目】春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过![]() 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍![]() ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )

A. 经过![]() 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到![]()
B. 室内空气中的含药量不低于![]() 的持续时间达到了
的持续时间达到了![]()
C. 当室内空气中的含药量不低于![]() 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D. 当室内空气中的含药量低于![]() 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到![]() 开始,需经过
开始,需经过![]() 后,学生才能进入室内
后,学生才能进入室内
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com