
科目: 来源: 题型:
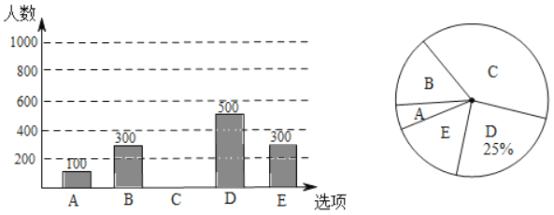
【题目】为调查遵义市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“![]() :自行车,
:自行车,![]() :电动车.
:电动车.![]() :公交车.
:公交车.![]() :家用汽车.E:其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
:家用汽车.E:其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)本次调查中,一共调查了____名市民:扇形统计图中,E项对应的扇形圆心角是______度;
(2)补全条形统计图;
(3)若甲、乙两人上班时从![]() 四种交通工具中随机选择一种.请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
四种交通工具中随机选择一种.请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
查看答案和解析>>
科目: 来源: 题型:
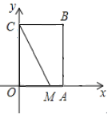
【题目】定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() ,点
,点![]() ,在边
,在边![]() 存在点
存在点![]() ,使得
,使得![]() 为“智慧三角形”,则点
为“智慧三角形”,则点![]() 的坐标为:______.
的坐标为:______.
查看答案和解析>>
科目: 来源: 题型:
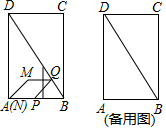
【题目】如图,在矩形ABCD中,AB=2cm,∠ADB=30°.P,Q两点分别从A,B同时出发,点P沿折线AB﹣BC运动,在AB上的速度是2cm/s,在BC上的速度是2![]() cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
(1)当PQ⊥AB时,x等于多少;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)直线AM将矩形ABCD的面积分成1:3两部分时,直接写出x的值.
查看答案和解析>>
科目: 来源: 题型:
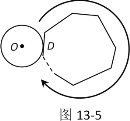
【题目】如图13-1至图13-5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c.
阅读理解:
(1)如图13-1,⊙O从⊙O1的位置出发,沿AB滚动到⊙O2的位置,当AB=c时,⊙O恰好自转1周.

(2)如图13-2,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋转的角∠O1BO2 = n°,⊙O在点B处自转![]() 周.
周.

实践应用:
(1)在阅读理解的(1)中,若AB=2c,则⊙O自转 周;若AB=l,则⊙O自转 周.在阅读理解的(2)中,若∠ABC= 120°,则⊙O在点B处自转 周;若∠ABC= 60°,则⊙O在点B处自转 周.
(2)如图13-3,∠ABC=90°,AB=BC=![]() c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.
c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.

拓展联想:
(1)如图13-4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
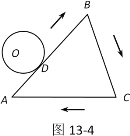
(2)如图13-5,多边形的周长为l,⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.
查看答案和解析>>
科目: 来源: 题型:
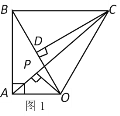
【题目】已知Rt△OAB,∠OAB=90o,∠ABO=30o,斜边OB=4,将Rt△OAB绕点O顺时针旋转60o,如图1,连接BC.
(1)ΔOBC的形状是 ;
(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;
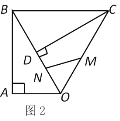
(3)如图2,点M、N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止.已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒.设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?(结果可保留根号) .

查看答案和解析>>
科目: 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为![]() (单位:km),乘坐地铁的时间
(单位:km),乘坐地铁的时间![]() (单位:min)是关于
(单位:min)是关于![]() 的一次函数,其关系如下表:
的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x/km | 7 | 9 | 11 | 12 | 13 |
y1/min | 16 | 20 | 24 | 26 | 28 |
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)李华骑单车的时间![]() (单位:min)也受
(单位:min)也受![]() 的影响,其关系可以用
的影响,其关系可以用![]() =
=![]()
![]() 2-11
2-11![]() +78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最时间.
+78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最时间.
查看答案和解析>>
科目: 来源: 题型:
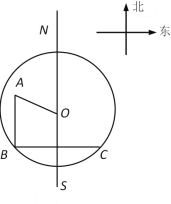
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.(本题参考数据:sin67.4°=![]() ,cos67.4°=
,cos67.4°=![]() ,tan67.4°=
,tan67.4°=![]() )
)
(1)求弦BC的长;
(2)请判断点A和圆的位置关系,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求平行四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com