
科目: 来源: 题型:
【题目】中考让同学们感觉压力较大,初三某班班主任想通过课间播放音乐来帮助学生缓解压力,采用全面调查的方法调查了学生对音乐类型的兴趣爱好,结果全班学生选择集中在流行音乐、民族音乐、摇滚音乐和轻音乐四种音乐类型.根据调查的结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
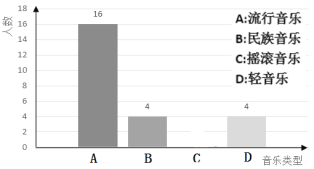
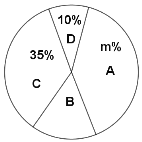
(1)求该班学生总人数,并把条形统计图补充完整;
(2)求扇形统计图中![]() 的值和表示流行音乐的扇形圆心角的度数;
的值和表示流行音乐的扇形圆心角的度数;
(3)班主任每天挑选出四种类型音乐各一首放在一个播放器内,每次随机播放两首不同音乐,请用画树状图或列表的方法求出某次恰好播放民族音乐和轻音乐的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() 的圆心在
的圆心在![]() 轴上,且半径均为
轴上,且半径均为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]()
![]()
![]() 射线
射线![]() 与
与![]() 相切于点
相切于点![]() ,射线
,射线![]() 与
与![]() 相切于点
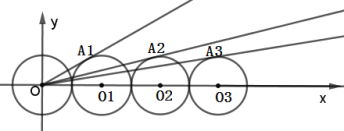
相切于点![]() ,按照这样的规律,
,按照这样的规律,![]() 的横坐标为_____.
的横坐标为_____.
查看答案和解析>>
科目: 来源: 题型:
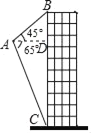
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).(参考数据:sin65°=0.91,cos65°=0.42,tan65°=2.14)
查看答案和解析>>
科目: 来源: 题型:
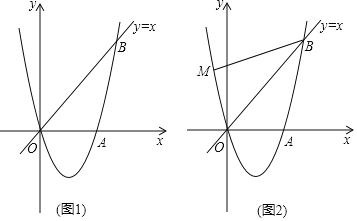
【题目】如(图1),已知经过原点的抛物线y=ax2+bx与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t)
,0),在第一象限内与直线y=x交于点B(2,t)
(1)求抛物线的解析式;
(2)在直线OB下方的抛物线上有一点C,点C到直线OB的距离为![]() ,求点C的坐标;
,求点C的坐标;
(3)如(图2),若点M在抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产的一种商品其售价是成本的1.5倍,当售价降低5元时商品的利润率为25%.若不进行任何推广年销售量为1万件.为了获得更好的利益,公司准备拿出一定的资金做推广,根据经验,每年投入的推广费x万元时销售量y(万件)是x的二次函数:当x为1万元时,y是1.5(万件).当x为2万元时,y是1.8(万件).
(1)求该商品每件的的成本与售价分别是多少元?
(2)求出年利润与年推广费x的函数关系式;
(3)如果投入的年推广告费为1万到3万元(包括1万和3万元),问推广费在什么范同内,公司获得的年利润随推广费的增大而增大?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校有![]() 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
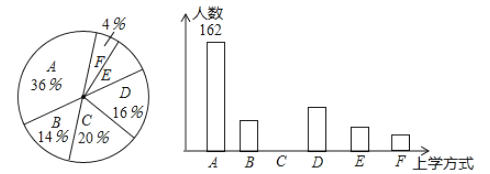
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择![]() 类的人数有_____人;
类的人数有_____人;
(2)在扇形统计图中,求![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)若将![]() 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
科目: 来源: 题型:
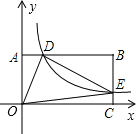
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=![]() (x>0)的图象与AB相交于点D.与BC相交于点E,且BD=3,AD=6,△ODE的面积为15,若动点P在x轴上,则PD+PE的最小值是_____.
(x>0)的图象与AB相交于点D.与BC相交于点E,且BD=3,AD=6,△ODE的面积为15,若动点P在x轴上,则PD+PE的最小值是_____.
查看答案和解析>>
科目: 来源: 题型:
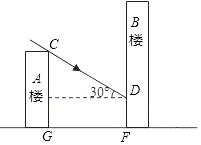
【题目】如图所示,小明家住在30米高的A楼里,小丽家住在B楼里,B楼坐落在A楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°.
(1)如果A、B两楼相距16![]() 米,那么A楼落在B楼上的影子有多长?
米,那么A楼落在B楼上的影子有多长?
(2)如果A楼的影子刚好不落在B楼上,那么两楼的距离应是多少米?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com