
科目: 来源: 题型:
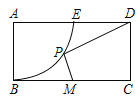
【题目】如图,矩形ABCD中,AB=2,AD=4,M点是BC的中点,A为圆心,AB为半径的圆交AD于点E.点P在弧BE上运动,则PM+![]() DP的最小值为____________.
DP的最小值为____________.
查看答案和解析>>
科目: 来源: 题型:
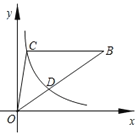
【题目】如图,△OBC的边BC∥x轴,过点C的双曲线y=![]() (k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
(k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
查看答案和解析>>
科目: 来源: 题型:
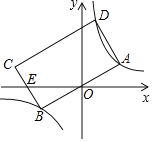
【题目】如图,矩形ABCD的顶点A,B,D分别落在双曲线y=![]() (k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
(k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
查看答案和解析>>
科目: 来源: 题型:
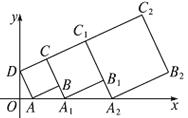
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2017个正方形的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】随着新冠肺炎的爆发,市场对口罩的需求量急剧增大.某口罩生产商自二月份以来,--直积极恢复产能,每日口罩生产量![]() (百万个)与天数
(百万个)与天数![]() 且
且![]() 为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数
为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数![]() 呈抛物线型,第
呈抛物线型,第![]() 天市场口罩缺口(需求量与供应量差)就达到
天市场口罩缺口(需求量与供应量差)就达到![]() (百万个),之后若干天,市场口罩需求量不断上升,在第
(百万个),之后若干天,市场口罩需求量不断上升,在第![]() 天需求量达到最高峰
天需求量达到最高峰![]() (百万个).
(百万个).
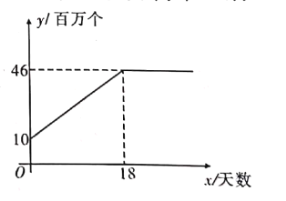
![]() 求出
求出![]() 与
与![]() 的函数解析式;
的函数解析式;
![]() 当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
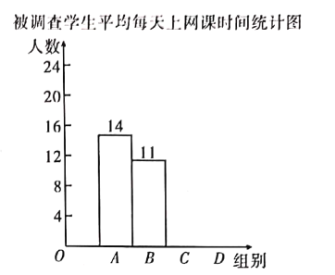
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.
查看答案和解析>>
科目: 来源: 题型:
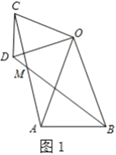
【题目】(1)问题发现:如图1,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交于点
交于点![]() .求证:
.求证:![]() ;并直接写出
;并直接写出![]() ______.
______.
(2)类比探究:如图2,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数.
的度数.
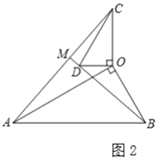
(3)拓展延伸:在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线
所在直线![]() 交于点.若
交于点.若![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目: 来源: 题型:
【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
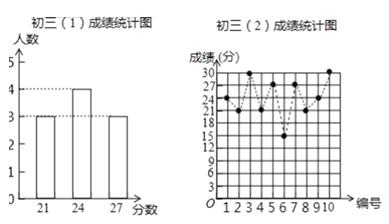
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 | 方差/分 |
初三(1)班 | 24 | 24 | ________ | 5.4 |
初三(2)班 | 24 | _________ | 21 | ________ |
(2)哪个班的学生纠错的得分更稳定?若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)现从两个班抽取了数学成绩最好的甲、乙、丙、丁四位同学,并随机分成两组进行数学竞赛,求恰好选中甲、乙一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com