
科目: 来源: 题型:
【题目】已知,如图1,在![]() 中,对角线
中,对角线![]() ,
,![]() ,
,![]() ,如图2,点
,如图2,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ;将
;将![]() 沿对角线
沿对角线![]() 剪开,
剪开,![]() 从图1的位置与点
从图1的位置与点![]() 同时出发,沿射线
同时出发,沿射线![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,当点
,当点![]() 停止运动时,
停止运动时,![]() 也停止运动.设运动时间为
也停止运动.设运动时间为![]() ,解答下列问题:
,解答下列问题:
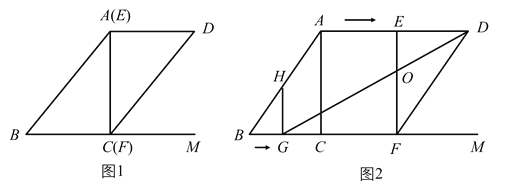
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)设四边形![]() 的面积为
的面积为![]() ,试确定
,试确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 有最大值?
有最大值?
(4)连接![]() ,试求当
,试求当![]() 平分
平分![]() 时,四边形
时,四边形![]() 与四边形
与四边形![]() 面积之比.
面积之比.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:
如图所示,有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上.

a.每次只能移动1个金属片;
b.较大的金属片不能放在较小的金属片上面.
把![]() 个金属片从1号针移到3号针,最少移动多少次?
个金属片从1号针移到3号针,最少移动多少次?
问题探究:为了探究规律,我们采用一般问题特殊化的方法,先从简单的情形入手,再逐次递进,最后得出一般性结论.
探究一:当![]() 时,只需把金属片从1号针移到3号针,用符号
时,只需把金属片从1号针移到3号针,用符号![]() 表示,共移动了1次.
表示,共移动了1次.
探究二:当![]() 时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动的顺序是:
时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动的顺序是:
a.把第1个金属片从1号针移到2号针;
b.把第2个金属片从1号针移到3号针;
c.把第1个金属片从2号针移到3号针.
用符号表示为:![]() ,
,![]() ,
,![]() .共移动了3次.
.共移动了3次.
探究三:当![]() 时,把上面两个金属片作为一个整体,则归结为
时,把上面两个金属片作为一个整体,则归结为![]() 的情形,移动的顺序是:
的情形,移动的顺序是:
a.把上面两个金属片从1号针移到2号针;
b.把第3个金属片从1号针移到3号针;
c.把上面两个金属片从2号针移到3号针.
其中(1)和(3)都需要借助中间针,用符号表示为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共移动了7次.
.共移动了7次.
(1)探究四:请仿照前面步骤进行解答:当![]() 时,把上面3个金属片作为一个整体,移动的顺序是:___________________________________________________.
时,把上面3个金属片作为一个整体,移动的顺序是:___________________________________________________.
(2)探究五:根据上面的规律你可以发现当![]() 时,需要移动________次.
时,需要移动________次.
(3)探究六:把![]() 个金属片从1号针移到3号针,最少移动________次.
个金属片从1号针移到3号针,最少移动________次.
(4)探究七:如果我们把![]() 个金属片从1号针移到3号针,最少移动的次数记为
个金属片从1号针移到3号针,最少移动的次数记为![]() ,当
,当![]() 时如果我们把
时如果我们把![]() 个金属片从1号针移到3号针,最少移动的次数记为
个金属片从1号针移到3号针,最少移动的次数记为![]() ,那么
,那么![]() 与
与![]() 的关系是
的关系是![]() __________.
__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:以下是我们教科书中的一段内容,请仔细阅读,并解答有关问题.
公元前3世纪,古希腊学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡,后来人们把它归纳为“杠杆原理”,通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂

(问题解决)
若工人师傅欲用撬棍动一块大石头,已知阻力和阻力臂不变,分别为1500N和0.4m.
(1)动力F(N)与动力臂l(m)有怎样的函数关系?当动力臂为1.5m时,撬动石头需要多大的力?
(2)若想使动力F(N)不超过题(1)中所用力的一半,则动力臂至少要加长多少?
(数学思考)
(3)请用数学知识解释:我们使用棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,山顶有一塔![]() ,塔高
,塔高![]() .计划在塔的正下方沿直线
.计划在塔的正下方沿直线![]() 开通穿山隧道
开通穿山隧道![]() .从与
.从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 、
、![]() 的仰角分别为
的仰角分别为![]() 、
、![]() ,从与
,从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 的仰角为
的仰角为![]() .求隧道
.求隧道![]() 的长度.(参考数据:
的长度.(参考数据:![]() ,
,![]() .)
.)
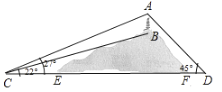
查看答案和解析>>
科目: 来源: 题型:
【题目】在学习“轴对称现象”内容时,老师让同学们寻找身边的轴对称图形,小明利用手中的一副三角尺和一个量角器(如图所示)进行探究.
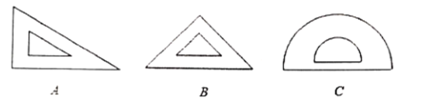
(1)小明在这三件文具中任取一件,结果是轴对称图形的概率是_________;(取三件中任意一件的可能性相同)
(2)小明发现在![]() 、
、![]() 两把三角尺中各选一个角拼在一起(无重叠无缝隙)会得到一个更大的角,若每个角选取的可能性相同,请用画树状图或列表的方法说明拼成的角是钝角的概率是多少.
两把三角尺中各选一个角拼在一起(无重叠无缝隙)会得到一个更大的角,若每个角选取的可能性相同,请用画树状图或列表的方法说明拼成的角是钝角的概率是多少.
查看答案和解析>>
科目: 来源: 题型:
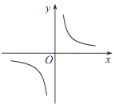
【题目】已知反比例函数 y=![]() 的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A.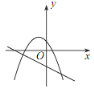 B.
B.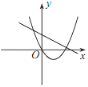 C.
C.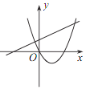 D.
D.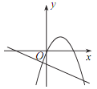
查看答案和解析>>
科目: 来源: 题型:
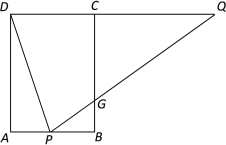
【题目】如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
(1)求证:DQ=PQ;
(2)求AP·DQ的最大值;
(3)若P为AB的中点,求PG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com