
科目: 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
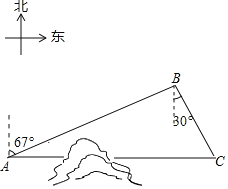
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)(参考数据:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校初级中学数学兴趣小组为了解本校学生年龄情况,随机调查了本校部分学生的年龄,根据所调查的学生的年龄(单位:岁),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
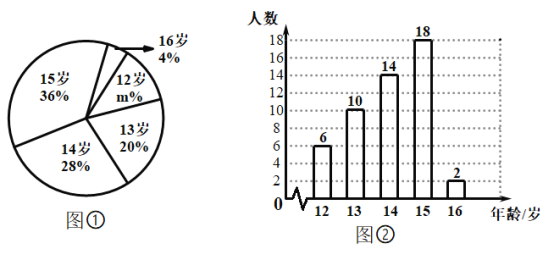
(1)本次接受调查的学生人数为_______,图①中 ![]() 的值为 ;
的值为 ;
(2)求统计的这组学生年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目: 来源: 题型:
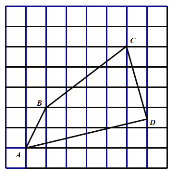
【题目】如图,在每个小正方形的边长为的网格中,点![]() 均在格点上,
均在格点上,![]() 为小正方形边中点.
为小正方形边中点.
(1)![]() 的长等于 ______;
的长等于 ______;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个点![]() ,使其满足
,使其满足![]() 说明点
说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目: 来源: 题型:
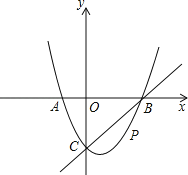
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)分别求出图中直线和抛物线的函数表达式;
(2)连接PO、PC,并把△POC沿C O翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
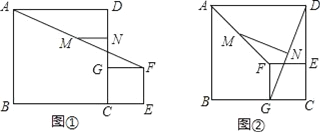
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)线段MN和GD的数量关系是_____,位置关系是_____;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
科目: 来源: 题型:
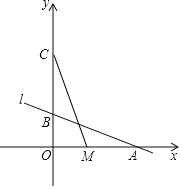
【题目】如图,直线l:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)将直线l向上平移4个单位后得到直线l',交y轴于点C.求直线l′的函数表达式;
(3)设点M的移动时间为t,当t为何值时,△COM≌△AOB,并求出此时点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
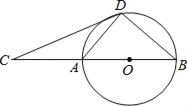
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若BC=6,tan∠CDA=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com