
科目: 来源: 题型:
【题目】如图,在A处的正东方向有一港口B.某巡艇从A处沿着北偏东60°方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.若取![]()
![]() 结果保留一位小数,则A,B间的距离为()
结果保留一位小数,则A,B间的距离为()
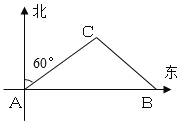
A.42.3海里B.73.5海里C.115.8海里D.119.9海里
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以边AB为直径的⊙O交边BC于点D,交边AC于点E.过D点作DF⊥AC于点F.
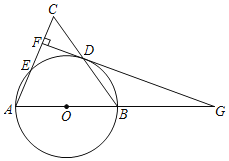
(1)求证:DF是⊙O的切线;
(2)求证:CF=EF;
(3)延长FD交边AB的延长线于点G,若EF=3,BG=9时,求⊙O的半径及CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数y=![]() (k≠0,x>0)的图象与直线y=4x相交于点C,过直线上点A(2,a)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=4BD.
(k≠0,x>0)的图象与直线y=4x相交于点C,过直线上点A(2,a)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=4BD.
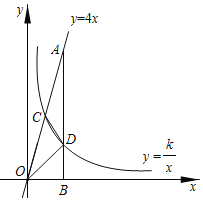
(1)求a的值;
(2)求k的值;
(3)连接OD,CD,求△OCD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】青白江凤凰湖湿地公园是一处具有国际水准的旅游度假区,以生态、休闲、水景环境及具有多国风情的建筑为特色.如图为凤凰湖湿地公园三个景点A,B,C的平面示意图,景点C在B的正北方向4千米处,景点A在B的东北方向,在C的北偏东75°方向上,求景点A、B之间的距离.(结果保留根号)
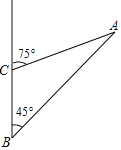
查看答案和解析>>
科目: 来源: 题型:
【题目】垃圾分类问题受到全社会的广泛关注,我区某校学生会向全校2100名学生发起了“垃圾要回家,请你帮助它”的捐款活动,用于购买垃圾分类桶.为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如图统计图1和图2,请根据相关信息,解答下列问题:
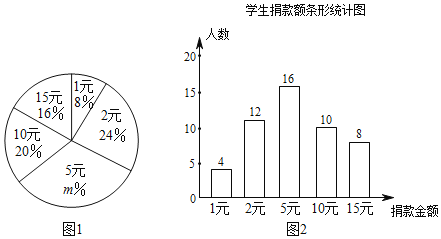
(1)本次接受随机抽样调查的学生人数为 ,图1中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为5元的学生人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与直线y=﹣x﹣2相交于A(﹣2,0),B(m,﹣6)两点,且抛物线经过点C (5,0).点P是直线下方的抛物线上异于A、B的动点.过点P作PD⊥x轴于点D,交直线于点E.
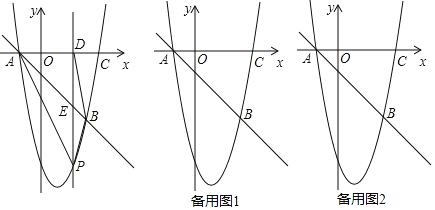
(1)求抛物线的解析式;
(2)连结PA、PB、BD,当S△ADB![]() S△PAB时,求S△PAB;
S△PAB时,求S△PAB;
(3)是否存在点P,使得△PBE为直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方形ABCD,过点B有一条直线1与正方形ABCD的对角线AC所在直线相交于点G,过点C、A分别作直线1的垂线段CE、AF于点E、F,对角线AC、BD相交于点O,连接OE、OF.
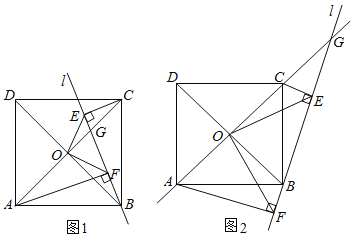
(1)如图1,猜测OE、OF有怎样的数量关系和位置关系,并说明理由;
(2)若正方形边长为10.
①若直线1在如图1的位置,当![]() 时,求EG的长;
时,求EG的长;
②若直线1在如图2的位置,当![]() 时,请直接写出EG的长.
时,请直接写出EG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①2a+b<0;
②﹣1≤a≤﹣![]() ;
;
③对于任意实数m,a(m2﹣1)+b(m﹣1)≤0总成立;
④关于x的方程ax2+bx+c=n+1有两个不相等的实数根.
其中结论正确的序号是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴的负半轴、y轴的正半轴上,点D在边BC上,将该矩形沿AD折叠,点B恰好落在边OC上的E处,且△CDE为等腰直角三角形,若OA=4,则点D的坐标是_____.
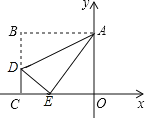
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,设二次函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图象经过点
的图象经过点![]() ,求函数
,求函数![]() 的表达式;
的表达式;
(2)若一次函数![]() 的图象与函数
的图象与函数![]() 的图象经过
的图象经过![]() 轴上同一点,探究实数
轴上同一点,探究实数![]() 满足的关系式;若
满足的关系式;若![]() 随
随![]() 的变化能取得最大值,证明:当
的变化能取得最大值,证明:当![]() 取得最大值时,抛物线
取得最大值时,抛物线![]() 与
与![]() 轴只有一个交点;
轴只有一个交点;
(3)已知点![]() 和
和![]() 在函数
在函数![]() 的图象上,若
的图象上,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com