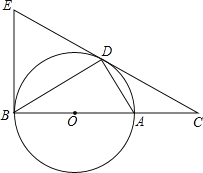
（1）求证：CD2=CACB；

（2）求证：CD是⊙O的切线；

（3）过点B作⊙O的切线交CD的延长线于点E，若BC=12，tan∠CDA=，求BE的长．

【题目】如图，直线：与轴、轴交于、两点，与反比例函数的图像交于点，且．

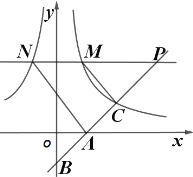
（1）求反比例函数的解析式；

（2）点是直线上一点，过点作轴的平行线交反比例函数和的图像于，两点，连，，当时，求的值．

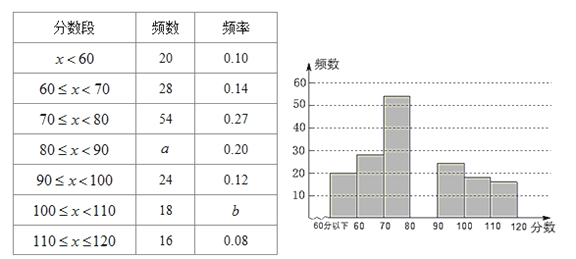
请根据以上图表提供的信息，解答下列问题：

（1）随机抽取部分学生的总人数是_________人，表格中的_________．

（2）请补全频数分布直方图；

（3）如果把成绩在90分以上(含90分)定为优秀，那么该市16000名九年级考生数学成绩为优秀的学生约有多少名？

【题目】有三个质地、大小都相同的小球分别标上数字2，－1，3后放入一个不透明的口袋搅匀，任意摸出一个小球，记下数字后，放回口袋中搅匀，再任意摸出一个小球，又记下数字b．这样就得到一个点的坐标．

（1）求这个点恰好在函数的图像上的概率．(请用“画树状图”或“列表”等方法给出分析过程，并求出结果)

（2）如果再往口袋中增加个标上数字2的小球，按照同样的操作过程，所得到的点恰好在函数的图像上的概率是_________(请用含的代数式直接写出结果)．

【题目】如图，在平面直角坐标系中，直线交轴于点，现将直线绕点顺时针方向旋转45°交轴于点，则直线的函数表达式是_________．

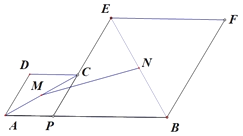
【题目】如图，已知，为线段上的一个动点，分别以，为边在的同侧作菱形和菱形，点，，在一条直线上，.，分别是对角线，的中点．当点在线段上移动时，点，之间的距离最短为(　　)

A.B.C.4D.3

【题目】如图，在平面直角坐标系中，已知点A（―3，6）、B（―9，一3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（ ）

A．（―1，2）

B．（―9，18）

C．（―9，18）或（9，―18）

D．（―1，2）或（1，―2）

【题目】在平面直角坐标系中，抛物线（）与轴交于A、B两点（点B在A的右侧），与轴交于点C，D是抛物线的顶点.

（1）当时，求顶点D 的坐标

（2）若OD = OB，求的值；

（3）设E为A，B两点间抛物线上的一个动点（含端点A，B），过点E作EH⊥轴，垂足为H，交直线BC于点F. 记线段EF的长为t，若t的最大值为，求的值.

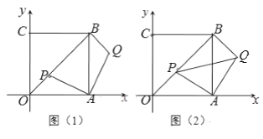
【题目】平面直角坐标系中，四边形OABC是正方形，点A，C 在坐标轴上，点B（，），P是射线OB上一点，将绕点A顺时针旋转90°，得，Q是点P旋转后的对应点.

（1）如图（1）当OP = 时，求点Q的坐标；

（2）如图（2），设点P（，）（），的面积为S. 求S与的函数关系式，并写出当S取最小值时，点P的坐标；

（3）当BP+BQ = 时，求点Q的坐标（直接写出结果即可）

（1）根据题意，填写下表：

（2）设一次购买种子的数量为 kg（）. 在甲店购买的付款金额记为元，在乙店购买的付款金额为元，分别求，关于的函数解析式；

（3） 若在同一店中一次购买种子的付款金额是36元，则最多可购买种子______ kg.若在同一店中一次购买种子10 kg，则最少付款金额是________元.