
科目: 来源: 题型:
【题目】下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为![]() ”的尺规作图过程.
”的尺规作图过程.
已知:![]() .求作:矩形
.求作:矩形![]() ,使得矩形
,使得矩形![]() 内接于
内接于![]() ,且其对角线
,且其对角线![]() 的夹角为
的夹角为![]() .
.
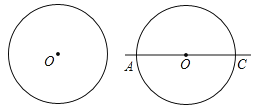
作法:如图,
①作![]() 的直径
的直径![]() ;
;
②以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 上方的圆弧于点
上方的圆弧于点![]() ;
;
③连接![]() 并延长交
并延长交![]() 于点
于点![]() ;
;
④连接![]() .
.
所以四边形![]() 就是所求作的矩形,根据小东设计的尺规作图过程,
就是所求作的矩形,根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹).
(2)完成下面的证明.
证明:∵点![]() 都在
都在![]() 上,
上,
∴![]() .
.
同理![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ( )(填推理的依据).
( )(填推理的依据).
∴四边形![]() 是矩形.
是矩形.
∵![]()
![]() ,
,
∴![]() .
.
∴四边形![]() 是所求作的矩形.
是所求作的矩形.
查看答案和解析>>
科目: 来源: 题型:
【题目】高速公路某收费站出城方向有编号为![]() 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
收费出口编号 |
|
|
|
|
|
通过小客车数量(辆) | 260 | 330 | 300 | 360 | 240 |
在![]() 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.
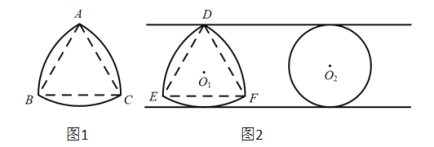
下列说法中错误的是( )
A.勒洛三角形是轴对称图形
B.图1中,点A到![]() 上任意一点的距离都相等
上任意一点的距离都相等
C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心![]() 的距离都相等
的距离都相等
D.图2中,勒洛三角形的周长与圆的周长相等
查看答案和解析>>
科目: 来源: 题型:
【题目】广阔无垠的太空中有无数颗恒星,其中离太阳系最近的一颗恒星称为“比邻星”,它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位,1光年约为9500000000000千米.则“比邻星”距离太阳系约为( )
A. ![]() 千米B.
千米B. ![]() 千米C.
千米C. ![]() 千米D.
千米D. ![]() 千米
千米
查看答案和解析>>
科目: 来源: 题型:
【题目】(操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°.

如图②,小明的作图方法如下:
第一步:分别以点A、B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA、OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于P1,P2.
所以图中P1,P2即为所求的点.
(1) 在图②中,连接P1A,P1 B,说明∠A P1B=30°;
(方法迁移)
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°.
(不写作法,保留作图痕迹)

(深入探究)
(3)已知矩形ABCD,BC=2,AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为 .
(4)已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解题
定义:如果四边形的某条对角线平分一组角,那么把这条对角线叫“美妙线”,该四边形叫做“美妙四边形”.
如图:在四边形ABCD中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫“美妙线”,四边形ABCD就称为“美妙四边形”.
问题:(1)下列四边形中是“美妙四边形”的有_______个.
①平行四边形 ②矩形 ③菱形 ④正方形
A.1 B. 2 C. 3 D.4
(2)四边形ABCD是“美妙四边形”,AB=3+![]() ,∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.
,∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.
(3)如图,若△ABC中,AB=3,BC=4,∠B=90°,将△ABC扩充成以AC为“美妙线”的“美妙四边形”ABCD,试求D到BC的距离.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是40元,根据市场调查:在一段时间内,销售单价是50元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>50),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | ① |
销售玩具获得利润ω(元) | ② |
(2)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于54元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
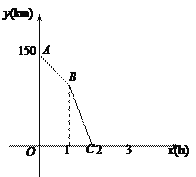
【题目】一辆货车从甲地出发以50 km/h的速度匀速驶往乙地,行驶1 h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8 h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.
(1)甲乙两地之间的距离是__________ km,轿车的速度是_________ km/h;
(2)求线段BC所表示的函数表达式;
(3)在图中画出货车与轿车相遇后的y(km)与x(h)的函数图像.
查看答案和解析>>
科目: 来源: 题型:
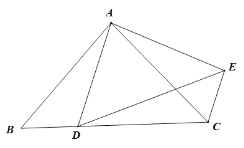
【题目】如图,在△ABC中,AB=AC,D是BC上任一点,AD=AE且∠BAC=∠DAE.
(1)若ED平分∠AEC,求证:CE∥AD;
(2)若∠BAC=90°,且D在BC中点时,试判断四边形ADCE的形状,并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com