
科目: 来源: 题型:
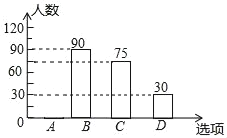
【题目】学校开展校外宣传活动,有社区板报(A)、集会演讲(B)、喇叭广播(C)、发宣传画(D)四种方式.围绕“你最喜欢的宣传方式”,校团委在全校学生中进行了抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下不完整的统计图表.
选项 | 方式 | 百分比 |
A | 社区板报 | m |
B | 集会演讲 | 30% |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共 人,m= ;
(2)若该校学生有900人,估计其中喜欢“集会演讲”宣传方式的学生约有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E,连接AD,BC,CO
(1)当∠BCO=25°时,求∠A的度数;
(2)若CD=4![]() ,BE=4,求⊙O的半径.
,BE=4,求⊙O的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB=12,C是线段AB上一点,分别以AC、CB为边在A的同侧作等边△ACP和等边△CBQ,连接PQ,则PQ的最小值是( )
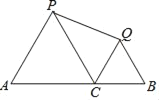
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目: 来源: 题型:
【题目】某机构调查了某小区部分居民当天行走的步数(单位:千步),并将数据整理绘制成如下不完整的频数直方图和扇形统计图.
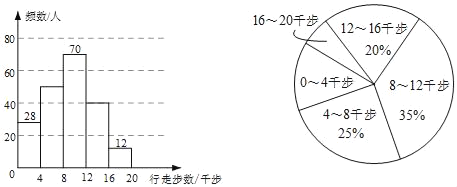
根据统计图,得出下面四个结论:
①此次一共调查了200位小区居民;
②行走步数为8~12千步的人数超过调查总人数的一半;
③行走步数为4~8千步的人数为50人;
④扇形图中,表示行走步数为12~16千步的扇形圆心角是72°.
其中正确的结论有( )
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD为矩形,AB=4cm,AD=3cm,动点M、N分别从D、B同时出发,都以1cm/秒的速度运动,点M沿DA向点终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于点P,连接MP,已知运动的时间为t秒(0<t<3).
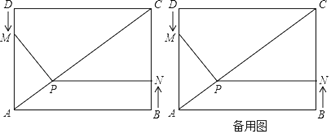
(1)当t=1秒时,求出PN的长;
(2)若四边形CDMP的面积为s,试求s与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t使四边形CDMP的面积与四边形ABCD的面积比为3:8,若存在,请求出t的值;若不存在,请说明理由.
(4)在点M、N运动过程中,△MPA能否成为一个等腰三角形?若能,试求出所有t的可能值;若不能,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
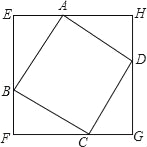
【题目】如图,正方形ABCD的四个顶点分别在正方形EFGH的四条边上,我们称正方形EFGH是正方形ABCD的外接正方形.
探究一:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍?如图,假设存在正方形EFGH,它的面积是正方形ABCD的2倍.
因为正方形ABCD的面积为1,则正方形EFGH的面积为2,
所以EF=FG=GH=HE=![]() ,设EB=x,则BF=
,设EB=x,则BF=![]() ﹣x,
﹣x,
∵Rt△AEB≌Rt△BFC
∴BF=AE=![]() ﹣x
﹣x
在Rt△AEB中,由勾股定理,得
x2+(![]() ﹣x)2=12
﹣x)2=12
解得,x1=x2=![]()
∴BE=BF,即点B是EF的中点.
同理,点C,D,A分别是FG,GH,HE的中点.
所以,存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍
探究二:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的3倍?(仿照上述方法,完成探究过程)
探究三:巳知边长为1的正方形ABCD, 一个外接正方形EFGH,它的面积是正方形ABCD面积的4倍?(填“存在”或“不存在”)
探究四:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的n倍?(n>2)(仿照上述方法,完成探究过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】6月1日是儿童节,为了迎接儿童节的到来,兰州某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
(3)在(2)条件下,若每件甲种玩具售价30元,每件乙种玩具售价45元,请求出卖完这批玩具获利W(元)与甲种玩具进货量m(件)之间的函数关系式,并求出最大利润为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在平行四边形中,点E在BC边上,连接AE.O为AE中点,连接BO并延长交AD于F.
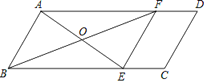
(1)求证:△AOF≌△BOE,
(2)判断当AE平分∠BAD时,四边形ABEF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
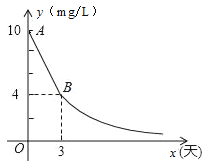
【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的浓度降为4 mg/L.从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y(mg/L) | 4 | 3 | 2.4 | 2 | 1.5 |
(1)求整改过程中当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0 mg/L?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次综合实践课上,同学们为教室窗户设计一个遮阳篷,小明同学绘制的设计图如图所示,其中AB表示窗户,且AB=2米,BCD表示直角遮阳蓬,已知当地一年中正午时刻太阳光与水平线CD的最小夹角∠PDN=18.6°,最大夹角∠MDN=64.5°.请你根据以上数据,帮助小明同学计算出遮阳篷中CD的长是多少米?(结果精确到0.1)(参考数据:sin18.6°≈0.32,tan18.6°≈0.34,sin64.5°≈0.90,tan64.5°≈2.1)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com