
科目: 来源: 题型:
【题目】阅读下列两则材料,回答问题:
材料一:因为![]() 所以我们将
所以我们将![]() 与
与![]() 称为一対“有理化因式”,有时我们可以通过构造“有理化因式”求值
称为一対“有理化因式”,有时我们可以通过构造“有理化因式”求值
例如:已知![]() ,求
,求![]() 的值
的值
解:![]() ,∵
,∵![]()
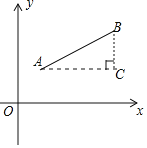
材料二:如图,点A(x1,y1),点B(x2,y2),所以AB为斜边作Rt△ABC,则C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,所以AB=![]() ,反之,可将代数式
,反之,可将代数式![]() 的值看作点(x1,y1)到点(x2,y2)的距离.例如
的值看作点(x1,y1)到点(x2,y2)的距离.例如![]() =
=![]() ,所以可将代数式
,所以可将代数式![]() 的值看作点(x,y)到点(1,﹣1)的距离;
的值看作点(x,y)到点(1,﹣1)的距离;
(1)利用材料一,解关于x的方程:![]() ,其中x≤2;
,其中x≤2;
(2)利用材料二,求代数式![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范围.
的最小值,并求出此时y与x的函数关系式,写出x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
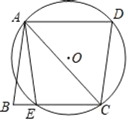
【题目】如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE.
(1)若∠D=78°,求∠EAC的度数.
(2)若∠EAC=α,则∠B的度数为 (直接用含α的式子表示)
查看答案和解析>>
科目: 来源: 题型:
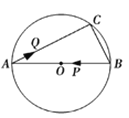
【题目】如图,AB是⊙O的直径,弦BC=6cm,AC=8cm.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目: 来源: 题型:
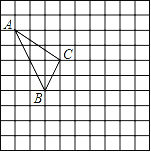
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 .
(4)△ABC的面积为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=![]() x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).
(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个

①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目: 来源: 题型:
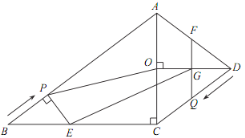
【题目】已知:如图,在四边形 ABCD 中, AB∥CD, ACB =90°, AB=10cm, BC=8cm, OD 垂直平分 A C.点 P 从点 B 出发,沿 BA 方向匀速运动,速度为 1cm/s;同时,点 Q 从点 D 出发,沿 DC 方向匀速运动,速度为 1cm/s;当一个点停止运动,另一个点也停止运动.过点 P作 PE⊥AB,交 BC 于点 E,过点 Q 作 QF∥AC,分别交 AD, OD 于点 F, G.连接 OP,EG.设运动时间为 t ( s )(0<t<5) ,解答下列问题:
(1)当 t 为何值时,点 E 在 BAC 的平分线上?
(2)设四边形 PEGO 的面积为 S(cm2) ,求 S 与 t 的函数关系式;
(3)在运动过程中,是否存在某一时刻 t ,使四边形 PEGO 的面积最大?若存在,求出t 的值;若不存在,请说明理由;
(4)连接 OE, OQ,在运动过程中,是否存在某一时刻 t ,使 OE⊥OQ?若存在,求出t 的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:
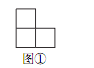
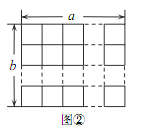
如图,图①是一张由三个边长为 1 的小正方形组成的“L”形纸片,图②是一张 a× b 的方格纸(a× b的方格纸指边长分别为 a,b 的矩形,被分成 a× b个边长为 1 的小正方形,其中 a≥2 , b≥2,且 a,b 为正整数) .把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
问题探究:
为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.
探究一:
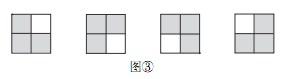
把图①放置在 2× 2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图③,对于 2×2的方格纸,要用图①盖住其中的三个小正方形,显然有 4 种不同的放置方法.
探究二:
把图①放置在 3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图④,在 3×2的方格纸中,共可以找到 2 个位置不同的 2 ×2方格,依据探究一的结论可知,把图①放置在 3×2 的方格纸中,使它恰好盖住其中的三个小正方形,共有 2 ×4=8种
不同的放置方法.
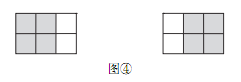
探究三:
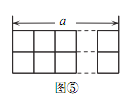
把图①放置在 a ×2 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图⑤, 在 a ×2 的方格纸中,共可以找到______个位置不同的 2×2方格,依据探究一的结论可知,把图①放置在 a× 2 的方格纸中,使它恰好盖住其中的三个小正方形,共有______种不同的放置方法.
探究四:
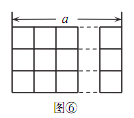
把图①放置在 a ×3 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图⑥,在 a ×3 的方格纸中,共可以找到______个位置不同的 2×2方格,依据探究一的结论可知,把图①放置在 a ×3 的方格纸中,使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
……
问题解决:
把图①放置在 a ×b的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.)
问题拓展:
如图,图⑦是一个由 4 个棱长为 1 的小立方体构成的几何体,图⑧是一个长、宽、高分别为 a,b ,c (a≥2 , b≥2 , c≥2 ,且 a,b,c 是正整数)的长方体,被分成了a×b×c个棱长为 1 的小立方体.在图⑧的不同位置共可以找到______个图⑦这样的几何体.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com