
科目: 来源: 题型:
【题目】“数学迷”小楠通过从“特殊到一般”的过程,对倍角三角形(一个内角是另一个内角的2倍的三角形)进行研究,得出结论:如图1,在![]() 中,
中,![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,如果
,如果![]() ,那么
,那么![]() .下面给出小楠对其中一种特殊情形的一种证明方法.
.下面给出小楠对其中一种特殊情形的一种证明方法.
已知:如图2,在△![]() 中,
中,![]() ,
,![]() .求证:
.求证:![]() .
.
证明:如图2,延长![]() 到
到![]() ,使得
,使得![]() .
.
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴△![]() △
△![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
根据上述材料提供的信息,请你完成下列情形的证明(用不同于材料中的方法也可以);
已知:如图1,在△![]() 中,
中,![]() .
.
求证:![]() .
.


查看答案和解析>>
科目: 来源: 题型:
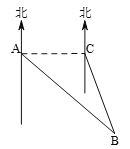
【题目】如图,小岛![]() 正好在深水港口
正好在深水港口![]() 的东南方向,一艘集装箱货船从港口
的东南方向,一艘集装箱货船从港口![]() 出发,沿正东方向以每小时30千米的速度行驶,40分钟后在
出发,沿正东方向以每小时30千米的速度行驶,40分钟后在![]() 处测得小岛
处测得小岛![]() 在它的南偏东
在它的南偏东![]() 方向,求小岛
方向,求小岛![]() 离深水港口
离深水港口![]() 的距离(精确到0.1千米).参考数据:
的距离(精确到0.1千米).参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
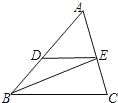
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果![]() =3,
=3,![]() =2,DE=6,求BC的长.
=2,DE=6,求BC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),已知∠![]() ,点
,点![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,
,![]() 、
、![]() 为射线
为射线![]() 和
和![]() 上的两个动点(
上的两个动点(![]() ),过点
),过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() ,且
,且![]() ,联结
,联结![]() .
.
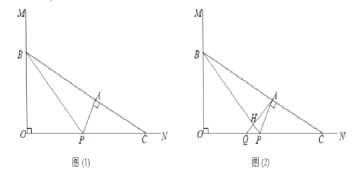
(1)若![]() 时,求
时,求![]() 的值;
的值;
(2)设![]() ,
,![]() 求
求![]() 与
与![]() 之间的函数解析式,并写出定义域;
之间的函数解析式,并写出定义域;
(3)如图(2),过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,交射线
,交射线![]() 于点
于点![]() ,点
,点![]() 、
、![]() 在射线
在射线![]() 和
和![]() 上运动时,探索线段
上运动时,探索线段![]() 的长是否发生变化?若不发生变化,求出它的值。若发生变化,试用含x的代数式表示
的长是否发生变化?若不发生变化,求出它的值。若发生变化,试用含x的代数式表示![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
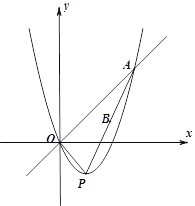
【题目】如图,已知直线![]() 与二次函数
与二次函数![]() 的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=
的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=![]() ,AP的中点为B.
,AP的中点为B.
(1)求二次函数的解析式;
(2)求线段OB的长;
(3)若射线OB上存在点Q,使得△AOQ与△AOP相似,求点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can).
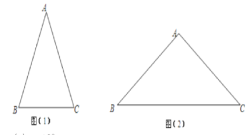
如图(1)在△![]() 中,
中,![]() ,底角
,底角![]() 的邻对记作
的邻对记作![]() ,这时
,这时![]() ,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义解下列问题:
,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义解下列问题:
(1)![]() = ;
= ;
(2)如图(2),在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,求△
,求△![]() 的周长
的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com