
科目: 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行一次分四个层次的抽样调查(四个层次为:A,非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同),并把调查结果绘制成如下两幅不完整的统计图,请根据统计图中的倍息解答下列问题:

(1)本次被抽查的居民人数是 人,将条形统计图补充完整.
(2)图中∠α的度数是 度;该小区有3000名居民,请估计对“广场舞”表示赞同(包括A层次和B层次)的大约有人
(3)据了解,甲、乙、丙、丁四位居民投不赞同票,小王想从这四位居民中随机选择两位了解具体情况,请用列表或画树状图的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰△ABC中,AB=BC,点D是AC边的中点,延长BD至点E,使得DE=BD,连结CE.
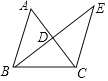
(1)求证:△ABD≌△CED.
(2)当BC=5,CD=3时,求△BCE的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在关于“折纸问题”的数学活动课中,小刚沿菱形纸片ABCD各边中点的连线裁剪得到四边形纸片EFGH,再将纸片EFGH按如图所示分别沿MN、P2折叠,使点E,G落在线段PN上点E,G处,当PNEF时,若阴影部分的周长之和为16,△AEH,△CFG的面积之和为12,则菱形纸片ABCD的一条对角线BD的长为_____.
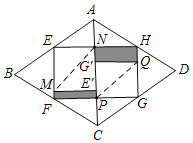
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在两建筑物之间有一高为15米的旗杆,从高建筑物的顶端A点经过旗杆顶点恰好看到矮建筑物的底端墙角C点,且俯角a为60°,又从A点测得矮建筑物左上角顶端D点的俯角β为30°,若旗杆底部点G为BC的中点(点B为点A向地面所作垂线的垂足)则矮建筑物的高CD为_____.
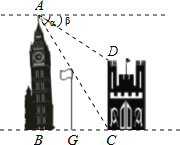
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() (x>0)图象上的两点,分别过A,B两点向x轴,y轴作垂线段,AD,BE两垂线段交于点G.若图中阴影部分的面积为3,则△OAB的面积为( )
(x>0)图象上的两点,分别过A,B两点向x轴,y轴作垂线段,AD,BE两垂线段交于点G.若图中阴影部分的面积为3,则△OAB的面积为( )
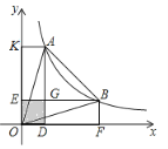
A.9B.10C.11D.12
查看答案和解析>>
科目: 来源: 题型:
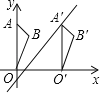
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(0,4)和(1,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A在直线y=![]() x﹣1上,则点B与点O′之间的距离为( )
x﹣1上,则点B与点O′之间的距离为( )
A.3B.4C.3![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() (b,c为常数)与x轴交于点
(b,c为常数)与x轴交于点![]() 和
和![]() ,与y轴交于点A,点E为抛物线顶点。
,与y轴交于点A,点E为抛物线顶点。
(Ⅰ)当![]() 时,求点A,点E的坐标;
时,求点A,点E的坐标;
(Ⅱ)若顶点E在直线![]() 上,当点A位置最高时,求抛物线的解析式;
上,当点A位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求b的值。
值最小时,求b的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() .
.
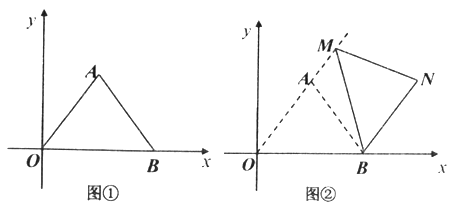
(Ⅰ)如图①,求AB的长;
(Ⅱ)如图②,把图①中的![]() 绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
①求证:![]() ;②求点N的坐标;
;②求点N的坐标;
(Ⅲ)点C是OB的中点,点D为线段OA上的动点,在![]() 绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
查看答案和解析>>
科目: 来源: 题型:
【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com