
科目: 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如下(未完成),解答下列问题:


(1)若A组的频数比B组小24,求频数分布直方图中的![]() 、
、![]() 的值;
的值;
(2)扇形统计图中,D部分所对的圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上为优秀,全校共有2000名学生,估计成绩优异的学生有多少名?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,A(1,2),B(3,4),C(4,1),连接AB、BC、CA,平移△ABC得到△DEF,其中A点与D点对应,B点与E点对应,C点与F点对应。
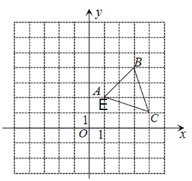
(1)使E与A重合,画出△DEF,并写出F的坐标;
(2)若将△ABC向左平移![]() 个单位,使得到的△DEF的顶点D、F分别位于
个单位,使得到的△DEF的顶点D、F分别位于![]() 轴两侧,求
轴两侧,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
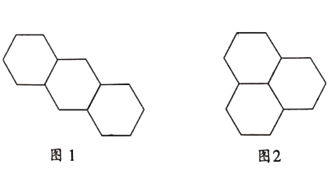
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是_______.有![]() 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则
个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也是300m,则大刚家相对于小亮家的位置是_______。

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知点E,F,G,H是矩形ABCD各边的中点,AB=2.4,BC=3.4.动点M从点A出发,沿A→B→C→D→A匀速运动,到点A停止,设点M运动的路程为x,点M到四边形EFGH的某一个顶点的距离为y,如果表示y关于x的函数关系的图象如图2所示,那么四边形EFGH的这个顶点是( )
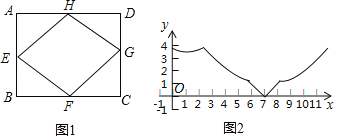
A. 点EB. 点FC. 点GD. 点H
查看答案和解析>>
科目: 来源: 题型:
【题目】数学课上,大家一起研究三角形中位线定理的证明,小丽和小亮在学习思考后各自尝试了一种辅助线,如图1,图2所示,其中辅助线做法能够用来证明三角形中位线定理的是( )

A. 小丽和小亮的辅助线做法都可以
B. 小丽和小亮的辅助线做法都不可以
C. 小丽的辅助线做法可以,小亮的不可以
D. 小亮的辅助线做法可以,小丽的不可以
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出;
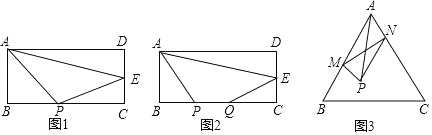
(1)如图1,矩形ABCD,AB=4,BC=8,点E为CD的中点,点P为BC上的动点,CP= 时,△APE的周长最小.
(2)如图2,矩形ABCD,AB=4,BC=8,点E为CD的中点,点P、点Q为BC上的动点,且PQ=2,当四边形APQE的周长最小时,请确定点P的位置(即BP的长)
问题解决;
(3)如图3,某公园计划在一片足够大的等边三角形水域内部(不包括边界)点P处修一个凉亭,设计要求PA长为100米,同时点M,N分别是水域AB,AC边上的动点,连接P、M、N的水上浮桥周长最小时,四边形AMPN的面积最大,请你帮忙算算此时四边形AMPN面积的最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
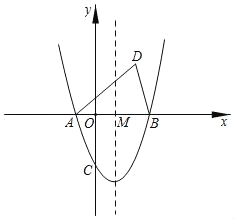
【题目】如图,抛物线y=x2+bx+c与x轴交于点A(﹣1,0)、B两点,与y轴交于点C(0,﹣3).
(1)求抛物线的函数解析式;
(2)已知点P(m,n)在抛物线上,当﹣2≤m<3时,直接写n的取值范围;
(3)抛物线的对称轴与x轴交于点M,点D与点C关于点M对称,试问在该抛物线上是否存在点P,使△ABP与△ABD全等?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com