
科目: 来源: 题型:
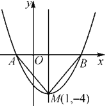
【题目】如图是二次函数y=x2+bx+c的图象,其顶点坐标为M(1,-4).
(1)求出图象与x轴的交点A、B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=![]() S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b>0;③-1≤ a ≤-![]() ;④4ac-b2>8a;(5)3a+c=0,其中正确的结论有( )个
;④4ac-b2>8a;(5)3a+c=0,其中正确的结论有( )个
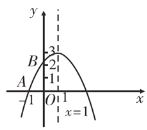
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线![]() 经过点
经过点![]() 、
、![]() 两点,
两点,![]() 是其顶点,将抛物线
是其顶点,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.
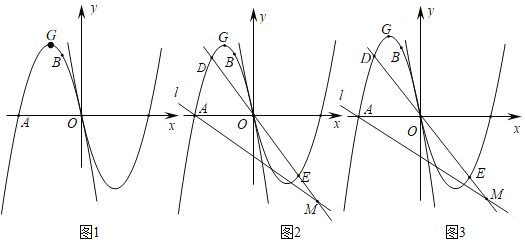
(1)求抛物线![]() 的函数解析式及顶点
的函数解析式及顶点![]() 的坐标;
的坐标;
(2)如图2,直线![]() 经过点
经过点![]() ,
,![]() 是抛物线
是抛物线![]() 上的一点,设
上的一点,设![]() 点的横坐标为
点的横坐标为![]() (
(![]() ),连接
),连接![]() 并延长,交抛物线
并延长,交抛物线![]() 于点
于点![]() ,交直线l于点
,交直线l于点![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)如图3,在(2)的条件下,连接![]() 、
、![]() ,在直线
,在直线![]() 下方的抛物线
下方的抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
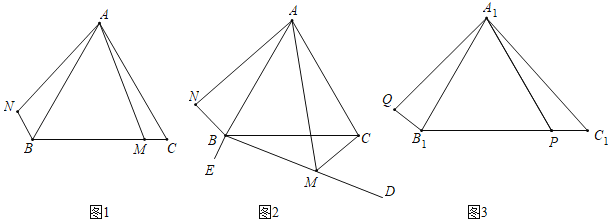
【题目】小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.
(一)猜测探究
在![]() 中,
中,![]() ,
,![]() 是平面内任意一点,将线段
是平面内任意一点,将线段![]() 绕点
绕点![]() 按顺时针方向旋转与
按顺时针方向旋转与![]() 相等的角度,得到线段
相等的角度,得到线段![]() ,连接
,连接![]() .
.
(1)如图1,若![]() 是线段
是线段![]() 上的任意一点,请直接写出
上的任意一点,请直接写出![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的数量关系是 ;
的数量关系是 ;
(2)如图2,点![]() 是
是![]() 延长线上点,若
延长线上点,若![]() 是
是![]() 内部射线
内部射线![]() 上任意一点,连接
上任意一点,连接![]() ,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
(二)拓展应用
如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的任意点,连接
上的任意点,连接![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() .求线段
.求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点![]() 、点
、点![]() 在直线
在直线![]() 上,反比例函数
上,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() .
.
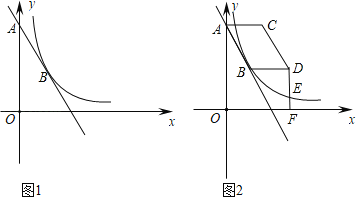
(1)求![]() 和
和![]() 的值;
的值;
(2)将线段![]() 向右平移
向右平移![]() 个单位长度(
个单位长度(![]() ),得到对应线段
),得到对应线段![]() ,连接
,连接![]() 、
、![]() .
.
①如图2,当![]() 时,过
时,过![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,求
,求![]() 的值;
的值;
②在线段![]() 运动过程中,连接
运动过程中,连接![]() ,若
,若![]() 是以
是以![]() 为腰的等腰三形,求所有满足条件的
为腰的等腰三形,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
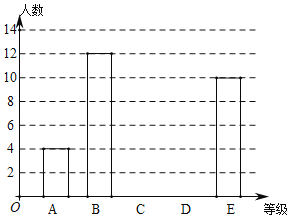
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买![]() 种图书花费了3000元,购买
种图书花费了3000元,购买![]() 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是![]() 种图书的1.5倍,购买
种图书的1.5倍,购买![]() 种图书的数量比
种图书的数量比![]() 种图书多20本.
种图书多20本.
(1)求![]() 和
和![]() 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了![]() 种图书20本和
种图书20本和![]() 种图书25本,共花费多少元?
种图书25本,共花费多少元?
查看答案和解析>>
科目: 来源: 题型:
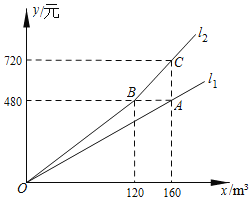
【题目】某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中![]() 、
、![]() 分别表示去年、今年水费
分别表示去年、今年水费![]() (元)与用水量
(元)与用水量![]() (
(![]() )之间的关系.小雨家去年用水量为150
)之间的关系.小雨家去年用水量为150![]() ,若今年用水量与去年相同,水费将比去年多_____元.
,若今年用水量与去年相同,水费将比去年多_____元.
查看答案和解析>>
科目: 来源: 题型:
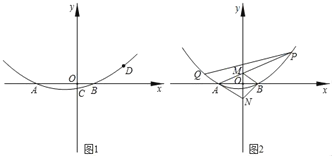
【题目】如图,抛物线y=ax2+bx﹣2a与x轴交于点A和点B(1,0),与y轴将于点C(0,﹣![]() ).
).
(1)求抛物线的解析式;
(2)若点D(2,n)是抛物线上的一点,在y轴左侧的抛物线上存在点T,使△TAD的面积等于△TBD的面积,求出所有满足条件的点T的坐标;
(3)直线y=kx﹣k+2,与抛物线交于两点P、Q,其中在点P在第一象限,点Q在第二象限,PA交y轴于点M,QA交y轴于点N,连接BM、BN,试判断△BMN的形状并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com