
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
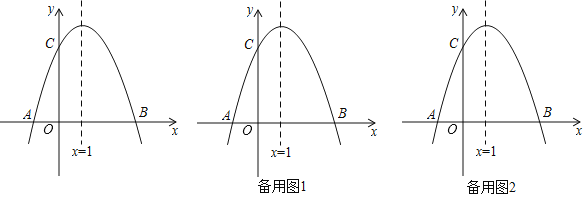
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①若![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的值;
的值;
②![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
科目: 来源: 题型:
【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度![]() ,他站在距离教学楼底部
,他站在距离教学楼底部![]() 处6米远的地面
处6米远的地面![]() 处,测得宣传牌的底部
处,测得宣传牌的底部![]() 的仰角为
的仰角为![]() ,同时测得教学楼窗户
,同时测得教学楼窗户![]() 处的仰角为
处的仰角为![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度![]() 的斜坡从
的斜坡从![]() 走到
走到![]() 处,此时
处,此时![]() 正好与地面
正好与地面![]() 平行.
平行.
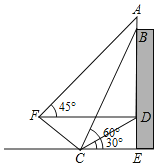
(1)求点![]() 到直线
到直线![]() 的距离(结果保留根号);
的距离(结果保留根号);
(2)若小明在![]() 处又测得宣传牌顶部
处又测得宣传牌顶部![]() 的仰角为
的仰角为![]() ,求宣传牌的高度
,求宣传牌的高度![]() (结果精确到0.1米,
(结果精确到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
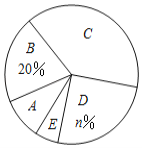
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=﹣5x+5与x轴,y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴的另一交点为B.
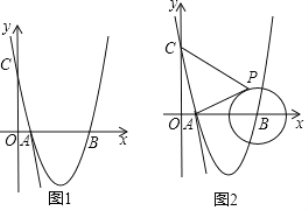
(1)求抛物线解析式及B点坐标;
(2)若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;
(3)如图2,若P点是半径为2的⊙B上一动点,连接PC、PA,当点P运动到某一位置时,PC+![]() PA的值最小,请求出这个最小值,并说明理由.
PA的值最小,请求出这个最小值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com