
科目: 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
, ![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙ O 的半径是![]() ,
,

①求出⊙ O 上的所有梦之点的坐标;
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】“十二五”以来,北京市人口增长过快导致城市不堪重负,是造成交通拥堵,能源匮乏等“大城市病”的根源之一.右图是根据北京市统计局近年各年末常住人口增长率及常住人口数的相关数据制作的统计图.

有下面四个判断:①从2011年至2016年,全市常住人口数在逐年下降; ②2010年末全市常住人口数达到近年来的最高值;③2015年末全市常住人口比2014年末增加18.9万人;④从2011年到2016年全市常住人口的年增长率连续递减。其中合理的是( )
A. ①② B. ①④ C. ②③ D. ③④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,且
,且![]() .
.
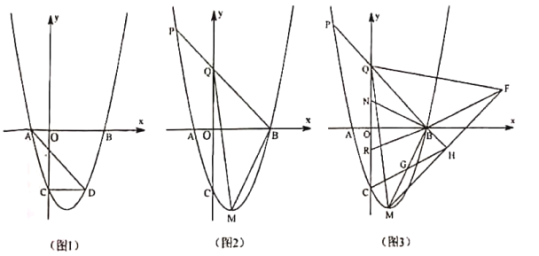
(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 为第二象限抛物线上一点,
为第二象限抛物线上一点,![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线的顶点,连接
为抛物线的顶点,连接![]() 、
、![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)如图3,在(2)的条件下,把![]() 沿直线
沿直线![]() 翻折使点
翻折使点![]() 落在点
落在点![]() 处,
处,![]() 与直线
与直线![]() 交于点
交于点![]() ,连接
,连接![]() 交线段
交线段![]() 于点
于点![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上(
上(![]() 上
上![]() 下),且
下),且![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:![]() 为
为![]() 直径,点
直径,点![]() 为
为![]() 上一点,弦
上一点,弦![]() ,垂足为
,垂足为![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,
,![]() .
.
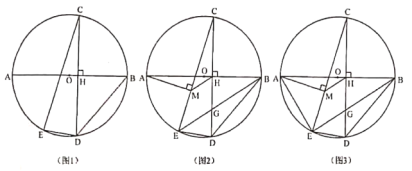
(1)如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】由于化工原料对人体健康的影响,所以某运输公司采用![]() 、
、![]() 两种机器人搬运化工原料,已知
两种机器人搬运化工原料,已知![]() 型机器人比
型机器人比![]() 型机器人每小时多搬运
型机器人每小时多搬运![]() ,
,![]() 型机器人搬运
型机器人搬运![]() 所用时间与
所用时间与![]() 型机器人搬运
型机器人搬运![]() 所用时间相等.
所用时间相等.
(1)求这两种机器人每小时分别搬运多少化工原料;
(2)该公司要搬运一批共计![]() 的化工原料,由于场地限制,两种机器人不能同时工作,公司要求不超过10小时完成搬运任务,请你帮该公司计算一下
的化工原料,由于场地限制,两种机器人不能同时工作,公司要求不超过10小时完成搬运任务,请你帮该公司计算一下![]() 型机器人至少需要工作多少小时.
型机器人至少需要工作多少小时.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 的垂线与过点
的垂线与过点![]() 的直线交于
的直线交于![]() 、
、![]() 两点.
两点.
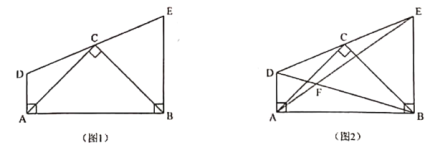
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() 、
、![]() 相交于点
相交于点![]() ,在不添加任何辅助线的情况下,请写出图2中的四对三角形,使写出的每对三角形面积相等.
,在不添加任何辅助线的情况下,请写出图2中的四对三角形,使写出的每对三角形面积相等.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解九年级学生的身高情况,随机抽取了部分学生的身高进行调查,利用所得数据绘成如下不完整的统计表和频数分布直方图,根据提供的信息解答下列问题:
身高分组( | 频数 | 百分比 |
| 5 |
|
|
| |
| 15 |
|
| 14 |
|
| 6 |
|
总计 |
|
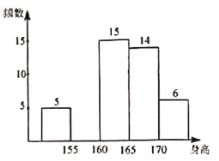
(1)![]() ______.
______.
(2)样本中位数所在组别为______.
(3)通过计算补全频数分布直方图;
(4)该校九年级共有300名学生,估计身高不低于![]() 的学生有多少人.
的学生有多少人.
查看答案和解析>>
科目: 来源: 题型:
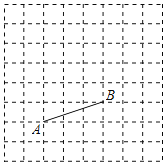
【题目】如图,在大小为![]() 的正方形方格中,线段
的正方形方格中,线段![]() 的两端点都在单位小正方形的顶点上.
的两端点都在单位小正方形的顶点上.
(1)在方格中画出一个![]() ,点
,点![]() 在小正方形的格点上使得
在小正方形的格点上使得![]() ,
,![]() .
.
(2)在方格中画出一个等腰![]() ,点
,点![]() 在小正方形的格点上,且使顶角为钝角,其面积等于4.
在小正方形的格点上,且使顶角为钝角,其面积等于4.
(3)在(1)(2)的条件下,连接![]() ,四边形
,四边形![]() 的面积为______个面积单位.
的面积为______个面积单位.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 是等边三角形,以点C为旋转中心,将线段CA按顺时针方向旋转
是等边三角形,以点C为旋转中心,将线段CA按顺时针方向旋转![]() 得到线段CD,连接BD交AC于点O.
得到线段CD,连接BD交AC于点O.
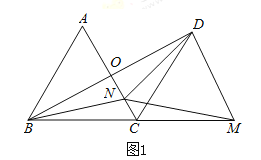
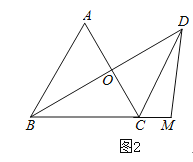
(1)如图1.
①求证:AC垂直平分BD;
②点M在BC的延长线上,点N在线段CO上,且![]() ,连接BN,判断
,连接BN,判断![]() 的形状,并加以证明;
的形状,并加以证明;
(2)如图2,点M在BC的延长线上,点N在线段AO上,且![]() ,补全图2,求证:
,补全图2,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
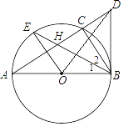
【题目】如图,AB是⊙O的直径,C是⊙O是一点,过点B作⊙O的切线,与AC延长线交于点D,连接BC,OE//BC交⊙O于点E,连接BE交AC于点H。(1)求证:BE平分∠ABC;(2)连接OD,若BH=BD=2,求OD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com