
科目: 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求该抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 平行于
平行于![]() 轴,交
轴,交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,试求出线段
,试求出线段![]() 的最大值,并写出此时点
的最大值,并写出此时点![]() 的坐标;
的坐标;
(3)抛物线上是否存在一点![]() ,使得
,使得![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() .
.
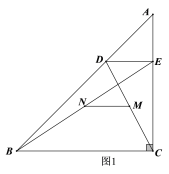

(1)问题发现
图1中,线段![]() 与线段
与线段![]() 之间的数量关系为_____________;
之间的数量关系为_____________;
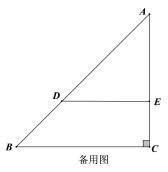
(2)类比探究
将![]() 绕点
绕点![]() 顺时针旋转到图2的位置,连接
顺时针旋转到图2的位置,连接![]() ,
,![]() .试问(1)中的结论是否仍然成立?请判断并说明理由;
.试问(1)中的结论是否仍然成立?请判断并说明理由;
(3)问题解决
若![]() ,将
,将![]() 绕点
绕点![]() 在平面内顺时针旋转,请直接写出线段
在平面内顺时针旋转,请直接写出线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了改善寄宿制学校学生的居住条件,某市财政局准备给部分学校加装空调.经市场调研发现:购买1台![]() 种型号的空调和2台
种型号的空调和2台![]() 种型号的空调共需资金6400元;购买2台
种型号的空调共需资金6400元;购买2台![]() 型空调和3台
型空调和3台![]() 型空调共需资金10600元.
型空调共需资金10600元.
(1)求![]() ,
,![]() 两种型号的空调单价各是多少元;
两种型号的空调单价各是多少元;
(2)现计划购进![]() ,
,![]() 两种型号的空调共200台,其中
两种型号的空调共200台,其中![]() 型空调为
型空调为![]() 台,并且要求公司15日内(含15日)完成安装调试.公司承诺:若
台,并且要求公司15日内(含15日)完成安装调试.公司承诺:若![]() 型空调不大于75台,则
型空调不大于75台,则![]() 型空调一定能保证15天内完成安装与调试,同时
型空调一定能保证15天内完成安装与调试,同时![]() 型空调每天可以完成10台的安装与调试;价格方面,当购买
型空调每天可以完成10台的安装与调试;价格方面,当购买![]() 型空调不少于60台时,公司给予
型空调不少于60台时,公司给予![]() 型空调7折优惠;当购买
型空调7折优惠;当购买![]() 型空调大于140台时,公司给予
型空调大于140台时,公司给予![]() 型空调8折优惠.若既能保证如期完成安装调试又能使花费资金最少,应购买
型空调8折优惠.若既能保证如期完成安装调试又能使花费资金最少,应购买![]() ,
,![]() 两种型号的空调各多少台?
两种型号的空调各多少台?
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() .分别以
.分别以![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,建立如图所示的平面直角坐标系.点
轴,建立如图所示的平面直角坐标系.点![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 的反比例函数
的反比例函数![]() 的图象与边
的图象与边![]() 交于点
交于点![]() .
.
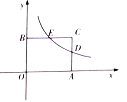
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)问在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 的值最小,若存在,请求出点
的值最小,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】核潜艇作为“三位一体”核打击力量中的一种,对于一个国家来说,是水下核威慑的重要战略武器.我国的核潜艇发展迅速,多次出色完成了战略巡航任务.一次,某型号核潜艇在水下400米的![]() 处以600米/分钟的速度向正东方向航行时,发现斜上方仰角为
处以600米/分钟的速度向正东方向航行时,发现斜上方仰角为![]() 水面上
水面上![]() 处有一可疑船只正沿着相同航向航行,跟踪2分钟后到达
处有一可疑船只正沿着相同航向航行,跟踪2分钟后到达![]() 处,再次测得可疑船只在仰角为
处,再次测得可疑船只在仰角为![]() 的
的![]() 处,请根据以上条件求出可疑船只航行的速度.(参考数据:
处,请根据以上条件求出可疑船只航行的速度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 外接圆的圆心,过点
外接圆的圆心,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
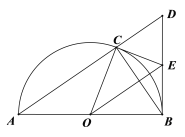
(1)求证:![]() ;
;
(2)填空:①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为平行四边形;
为平行四边形;
②当![]() 时,
时,![]() 的值为____________.
的值为____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市正在开展“太极拳进校园”活动,为了解学生太极拳的练习情况,随机抽取了部分学校学生进行问卷调查,将调查结果按照“![]() 每周练习6次或7次,
每周练习6次或7次,![]() 每周练习4次或5次,
每周练习4次或5次,![]() 每周练习2次或3次,
每周练习2次或3次,![]() 每周练习0次或1次”四类分别进行统计,并绘制了下列两幅尚不完整的统计图.
每周练习0次或1次”四类分别进行统计,并绘制了下列两幅尚不完整的统计图.
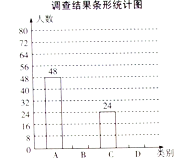
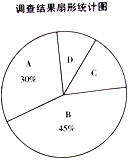
请根据图中信息,解答下列问题:
(1)此次共调查了___________名学生;
(2)在扇形统计图中,扇形![]() 的圆心角度数为__________;
的圆心角度数为__________;
(3)请将条形统计图补充完整;
(4)若该市约有30万名学生,请你估计每周练习太极拳不少于4次的学生的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年4月23日是中国海军成立70周年的日子,我国在山东青岛举行了国际海上大阅兵.为增强爱国意识,某校以此次大阅兵为契机,开展了“学习海军知识,增强爱国意识”答题比赛,进入决赛的10名同学的答题情况(共7道题)如下表所示:
答对题目数量(道) | 3 | 4 | 5 | 6 | 7 |
人数(人) | 1 | 2 | 4 | 2 | 1 |
则关于答对题目数量,下列说法正确的是( )
A.平均数是2.5B.中位数是4.5C.众数是5D.方差是4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+8与x轴交于A、B两点,交y轴于点C,连接BC,且点D坐标为(﹣2,4),tan∠OBC=![]() .
.
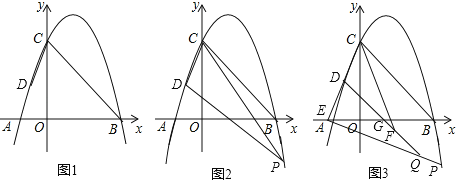
(1)求抛物线的解析式;
(2)P为第四象限抛物线上一点,连接PC、PD,设点P的横坐标为t,△PCD的面积为S,求S与t的函数关系式;
(3)延长CD交x轴于点E,连接PE,直线DG与x轴交于点G,与PE交于点Q,且OG=2,点F在DQ上,∠DQE+∠BCF=45°,若FQ=2![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ADBC内接于⊙O,AB为⊙O的直径,对角线AB、CD相交于点E.
(1)求证:∠BCD+∠ABD=90°;
(2)点G在AC的延长线上,连接BG,交⊙O于点Q,CA=CB,∠ABD=∠ABG,作GH⊥CD,交DC的延长线于点H,求证:GQ=![]() GH.
GH.
(3)在(2)的条件下,过点B作BF∥AD,交CD于点F,GH=3CH,若CF=4![]() ,求⊙O的半径.
,求⊙O的半径.
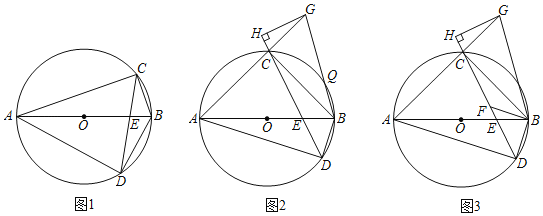
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com