
科目: 来源: 题型:
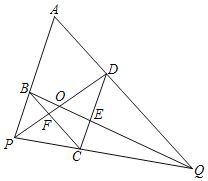
【题目】如图, 已知菱形![]() ,
,![]() ,点
,点![]() 是边
是边![]() 延长线上一点, 连接
延长线上一点, 连接![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式, 并写出它的定义域;
的函数解析式, 并写出它的定义域;
(3)当![]() 与
与![]() 相似时, 求
相似时, 求![]() 的值 .
的值 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图.在平面直角坐标系中.抛物线y=![]() x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
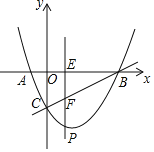
(1)求该抛物线的表达式;
(2)当线段EF,PF的长度比为1:2时,请求出m的值;
(3)是否存在这样的m,使得△BEP与△ABC相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
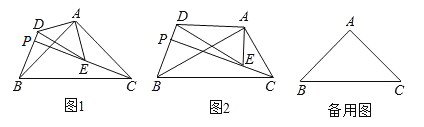
(1)问题提出:如图1,若AD=AE,AB=AC.
①∠ABD与∠ACE的数量关系为 ;②∠BPC的度数为 .
(2)猜想论证:如图2,若∠ADE=∠ABC=30°,则(1)中的结论是否成立?请说明理由.
(3)拓展延伸:在(1)的条件中,若AB=2,AD=1,若把△ADE绕点A旋转,当∠EAC=90°时,直接写出PB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.
(1)种植A,B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
查看答案和解析>>
科目: 来源: 题型:
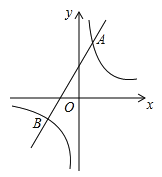
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.
查看答案和解析>>
科目: 来源: 题型:
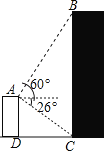
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:![]() ≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com