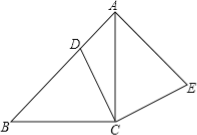
（1）求证：AB⊥AE；

（2）若BC2=ADAB，求证：四边形ADCE为正方形．

①画出△ABC向下平移4个单位长度得到的△A1B1C1 ， 点C1的坐标是________；

②以点B为位似中心，在网格内画出△A2B2C2 ， 使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是________；

③若M（a，b）为线段AC上任一点，写出点M的对应点M2的坐标________．

小芳：测得一根长为1米的竹竿的影长为0.8米，甲树的影长为4米（如图1）．

小华：发现乙树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图2），墙壁上的影长为1.2米，落在地面上的影长为2.4米．

小丽：测量的丙树的影子除落在地面上外，还有一部分落在教学楼的第一级台阶上（如图3），测得此影子长为0.3米，一级台阶高为0.3米，落在地面上的影长为4.5米．

（1）在横线上直接填写甲树的高度为 米．

（2）求出乙树的高度．

（3）请选择丙树的高度为（ ）

A、6.5米 B、5. 5米 C、6.3米 D、4.9米

A.2B.4C.D.2

甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似．

乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形相似．

对于两人的观点，下列说法正确的是（ ）

A．甲对，乙不对 B．甲不对，乙对 C．两人都对 D．两人都不对

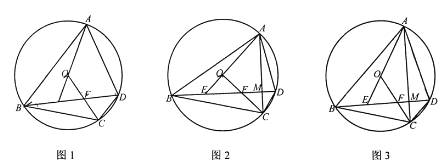
（1）求证：BE=FD；

（2）如图2，若∠EOF=90°，BE=EF，⊙O的半径，求四边形ABCD的面积；

（3）如图3，若AD=BC；

①求证：；②若，直接写出CD的长.

【题目】有三个函数，对于同一个自变量x，对应的函数值分别为，若恰好有，则称y为的“中值函数”.

（1）若的图像为直线，的图像是抛物线，则它们的中值函数的图像为（ ）

A.直线 B.抛物线 C.双曲线 D.以上答案均错

（2）若、它们的中值函数为，

①若点P在、和它们的中值函数图像上，则点P的坐标为_________.

②在如图中，画出上述中值函数的大致图象.并根据图象写出这个中值函数的两条性质；

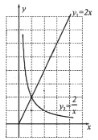
性质1：_______________________________；

性质2：_______________________________；

③利用中值函数的性质说明：面积为1的长方形，当该长方形长与宽相等时，周长最小.

(1)小颖和小红在实验中如果各掷一枚骰子，那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明，并求出其最大概率。

(2)他们在一次实验中共掷骰子60次，试验的结果如下：

①填空：此次实验中“5点朝上”的频率为______；

②小红说：“根据实验，出现5点朝上的概率最大。”她的说法正确吗?为什么?

（1）求证：△BGF∽△DHE；

（2）求BF的长．

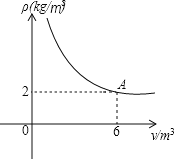
（1）求密度ρ关于体积V的函数解析式；

（2）当密度ρ不低于4kg/m3时，求二氧化碳体积的取值范围。