
科目: 来源: 题型:
【题目】如图,抛物线![]() (
(![]() 、
、![]() 、
、![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)如图,在直线![]() 下方的抛物线上是否存在点
下方的抛物线上是否存在点![]() 使四边形
使四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
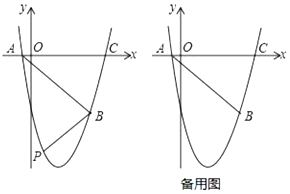
(3)若点![]() 为抛物线的对称轴上的一个动点,试指出
为抛物线的对称轴上的一个动点,试指出![]() 为等腰三角形的点
为等腰三角形的点![]() 共有几个?并求以
共有几个?并求以![]() 为底边时,点
为底边时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
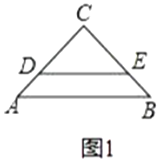
【题目】如图1,将两个等腰三角形![]() 和
和![]() 拼合在一起,其中
拼合在一起,其中![]() ,
,![]() ,
,![]() .
.
(1)操作发现
如图2,固定![]() ,把
,把![]() 绕着顶点
绕着顶点![]() 旋转,使点
旋转,使点![]() 落在
落在![]() 边上.
边上.
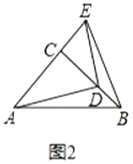
填空:线段![]() 与
与![]() 的关系是①位置关系:______;②数量关系:______
的关系是①位置关系:______;②数量关系:______
(2)变式探究
当![]() 绕点
绕点![]() 旋转到图3的位置时,(1)中的结论还成立吗?请说明理由;
旋转到图3的位置时,(1)中的结论还成立吗?请说明理由;
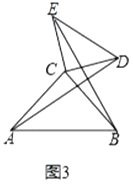
(3)解决问题
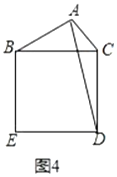
如图4,已知线段![]() ,线段
,线段![]() ,以
,以![]() 为边作一个正方形
为边作一个正方形![]() ,连接
,连接![]() ,随着边
,随着边![]() 的变化,线段
的变化,线段![]() 的长也会发生变化.请直接写出线段
的长也会发生变化.请直接写出线段![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店购进一种商品,每件商品进价为30元,试销中发现:销售价格为36元/件时,每天销售28件;销售价格为32元/件时,每天销售36件.若这种商品的销售量![]() (件)与销售价格
(件)与销售价格![]() (元)存在一次函数,请回答下列问题:
(元)存在一次函数,请回答下列问题:
(1)求出![]() 与
与![]() 的关系式;
的关系式;
(2)设商店销售这种商品每天获利![]() (元),写出
(元),写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
①当商店销售这种商品每天获利150元,销售价格定为多少比较合理;
②销售价格定为多少时,商店获利最大,最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给![]() 人.
人.
(1)求第一轮后患病的人数;(用含![]() 的代数式表示)
的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
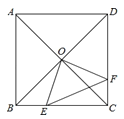
【题目】如图,正方形![]() 中,
中,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 两点同时出发,以
两点同时出发,以![]() 的速度沿
的速度沿![]() ,
,![]() 运动,到点
运动,到点![]() ,
,![]() 时停止运动,设运动时间为
时停止运动,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
A. B.
B.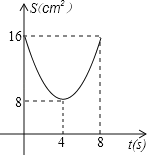 C.
C.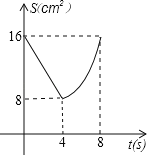 D.
D.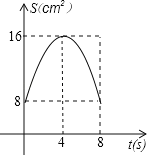
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一幅长为60 cm,宽为40 cm的矩形风景画的四周镶一条相同宽度的纸边,制成一幅矩形挂图.若要使整个挂图的面积是3 500 cm2,设纸边的宽为x cm,则根据题意可列方程为( )

A. (60+x)(40+x)=3 500 B. (60+2x)(40+2x)=3 500
C. (60-x)(40-x)=3 500 D. (60-2x)(40-2x)=3 500
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示).
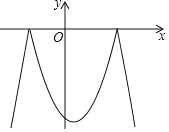
(1)求二次函数y=﹣x2+x+6的顶点坐标和x轴的交点坐标;
(2)直接写出新函数对应的解析式;
(3)当直线y=﹣x+m与新图象有四个交点时,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在扇形CAB中,CD⊥AB,垂足为D,圆E是△ACD的内切圆,切点分别为M,N,F,连接AE,BE.
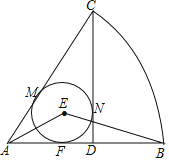
(1)求∠AEB的度数;
(2)若AD=DB,CD=3,求扇形CAB的弧长和圆E的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
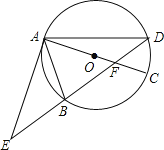
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似.
查看答案和解析>>
科目: 来源: 题型:
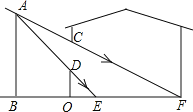
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.9m,窗高CD=1.1m,并测得OE=0.9m,OF=3m,求围墙AB的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com