
科目: 来源: 题型:
【题目】对于一个函数,自变量![]() 取
取![]() 时,函数值
时,函数值![]() 也等于
也等于![]() ,则称
,则称![]() 是这个函数的不动点.
是这个函数的不动点.
已知二次函数![]() .
.
(1)若3是此函数的不动点,则![]() 的值为__________.
的值为__________.
(2)若此函数有两个相异的不动点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的取值范围为__________.
的取值范围为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,直径
中,直径![]() 垂直弦
垂直弦![]() 于点
于点![]() ,且
,且![]() .点
.点![]() 为
为![]() 上一点(点
上一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连结
重合),连结![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .过点
.过点![]() 作
作![]() 于点
于点![]() .给出下列结论:①
.给出下列结论:①![]() 是等边三角形;②在点
是等边三角形;②在点![]() 从
从![]() 的运动过程中,
的运动过程中,![]() 的值始终等于
的值始终等于![]() .则下列说法正确的是( )
.则下列说法正确的是( )
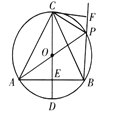
A.①,②都对B.①对,②错C.①错,②对D.①,②都错
查看答案和解析>>
科目: 来源: 题型:
【题目】对于给定函数y=a1x2+b1x+c1(其中a1、b1、c1为常数,且a1≠0),则称函数y= (a1=a2,b1+b2=0,c1+c2=0)为函数y=a1x2+b1x+c1(其中a1,b1,c1为常数,且a1≠0)的“相关函数”,此“相关函数”的图象记为G.
(a1=a2,b1+b2=0,c1+c2=0)为函数y=a1x2+b1x+c1(其中a1,b1,c1为常数,且a1≠0)的“相关函数”,此“相关函数”的图象记为G.
(1)已知函数y=﹣x2+4x+2.
①直接写出这个函数的“相关函数”;
②若点P(a,1)在“相关函数”的图象上,求a的值;
③若直线y=m与图象G恰好有两个公共点,直接写出m的取值范围;
(2)设函数y=﹣![]() x2+nx+1(n>0)的相关函数的图象G在﹣4≤x≤2上的最高点的纵坐标为y0,当
x2+nx+1(n>0)的相关函数的图象G在﹣4≤x≤2上的最高点的纵坐标为y0,当![]() ≤y0≤9时,直接写出n的取值范围.
≤y0≤9时,直接写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(0,﹣3)、B(﹣1,0)、C(2,﹣3),抛物线与x轴的另一交点为点E,点P为抛物线上一动点,设点P的横坐标为t.
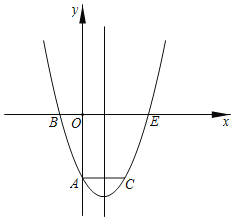
(1)求抛物线的解析式;
(2)若点P在第一象限,点M为抛物线对称轴上一点,当四边形MBEP恰好是平行四边形时,求点P的坐标;
(3)若点P在第四象限,连结PA、PE及AE,当t为何值时,△PAE的面积最大?最大面积是多少?
(4)是否存在点P,使△PAE为以AE为直角边的直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.如图所示,图中点的横坐标表示科技馆从8:30开门后经过的时间(分钟),纵坐标表示到达科技馆的总人数.图中曲线对应的函数解析式为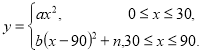 ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
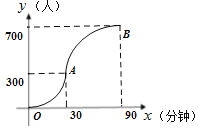
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
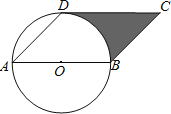
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2(a≠0).
(1)该二次函数图象的对称轴是直线 ;
(2)若该二次函数的图象开口向上,当﹣1≤x≤5时,函数图象的最高点为M,最低点为N,点M的纵坐标为![]() ,求点M和点N的坐标;
,求点M和点N的坐标;
(3)若该二次函数的图象开口向下,对于该二次函数图象上的两点A(x1,y1)、B(x2,y2),当x2≥3时,均有y1≥y2,请结合图象,直接写出x1的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com