
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在![]() 轴,
轴,![]() 轴的正半轴上.函数
轴的正半轴上.函数![]() 的图象与CB交于点D,函数
的图象与CB交于点D,函数![]() (
(![]() 为常数,
为常数,![]() )的图象经过点D,与AB交于点E,与函数
)的图象经过点D,与AB交于点E,与函数![]() 的图象在第三象限内交于点F,连接AF、EF.
的图象在第三象限内交于点F,连接AF、EF.
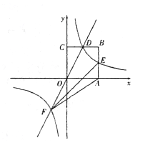
(1)求函数![]() 的表达式,并直接写出E、F两点的坐标.
的表达式,并直接写出E、F两点的坐标.
(2)求△AEF的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在校园文化艺术节中,九年级(1)班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,恰好选到男生是 事件(填随机或必然),选到男生的概率是 .
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图的方法,求刚好是一男生和一女生的概率.
查看答案和解析>>
科目: 来源: 题型:
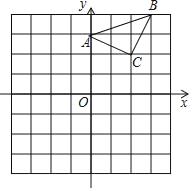
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上的一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则下列结论中:

①![]() ;②
;②![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④
;④![]() 正确的是()
正确的是()
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目: 来源: 题型:
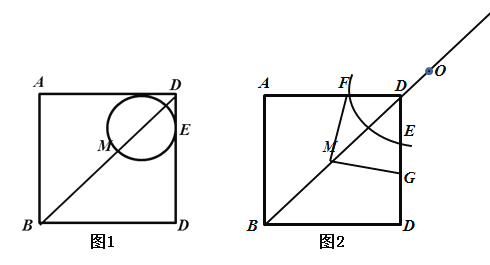
【题目】已知正方形ABCD的边长为2,中心为M,⊙O的半径为r,圆心O在射线BD上运动,⊙O与边CD仅有一个公共点E.
(1)如图1,若圆心O在线段MD上,点M在⊙O上,OM=DE,判断直线AD与⊙O的位置关系,并说明理由;
(2)如图2,⊙O与边AD交于点F,连接MF,过点M作MF的垂线与边CD交于点G,若![]() ,设点O与点M之间的距离为
,设点O与点M之间的距离为![]() ,EG=
,EG=![]() ,当
,当![]() 时,求
时,求![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() ,直线
,直线![]()
(1)当m=0时,若直线![]() 经过此抛物线的顶点,求b的值
经过此抛物线的顶点,求b的值
(2)将此抛物线夹在![]() 之间的部分(含交点)图象记为
之间的部分(含交点)图象记为![]() ,若
,若![]() ,
,
①判断此抛物线的顶点是否在图象![]() 上,并说明理由;
上,并说明理由;
②图象![]() 上是否存在这样的两点:
上是否存在这样的两点:![]() ,其中
,其中![]() ?若存在,求相应的
?若存在,求相应的![]() 和
和![]() 的取值范围
的取值范围
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
小辉和小乐一起在学校寄宿三年了,毕业之际,他们想合理分配共同拥有的三件“财产”:一个电子词典、一台迷你唱机、一套珍藏版小说.他们本着“在尊重各自的价值偏好基础上进行等值均分”的原则,设计了分配方案,步骤如下(相应的数额如表二所示):
①每人各自定出每件物品在心中所估计的价值;
②计算每人所有物品估价总值和均分值(均分:按总人数均分各自估价总值);
③每件物品归估价较高者所有;
④计算差额(差额:每人所得物品的估价总值与均分值之差);
⑤小乐拿225元给小辉,仍“剩下”的300元每人均分.
依此方案,两人分配的结果是:小辉拿到了珍藏版小说和375元钱,小乐拿到的电子词典和迷你唱机,但要付出375元钱.
(1)甲、乙、丙三人分配A,B,C三件物品,三人的估价如表三所示,依照上述方案,请直接写出分配结果;
(2)小红和小丽分配D,E两件物品,两人的估价如表四所示(其中0<m-n<15).按照上述方案的前四步操作后,接下来,依据“在尊重各自的价值偏好基础上进行等值均分”的原则,该怎么分配较为合理?请完成表四,并写出分配结果.(说明:本题表格中的数值的单位均为“元”)

查看答案和解析>>
科目: 来源: 题型:
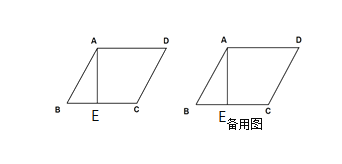
【题目】如图,在平行四边形ABCD中,AE⊥BC于点E.若一个三角形模板与△ABE完全重合地叠放在一起,现将该模板绕 点E顺时针旋转.要使该模板旋转60°后,三个顶点仍在平行四边形ABCD的边上,请探究平行四边形ABCD的角和边需要满足的条件.
查看答案和解析>>
科目: 来源: 题型:
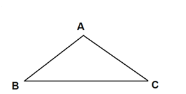
【题目】如图,在△ABC中,AB=AC.
(1)若以点A为圆心的圆与边BC相切于点D,请在下图中作出点D;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若该圆与边AC相交于点E,连接DE,当∠BAC=100°时,求∠AED的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某日6时至10时,某交易平台上一种水果的每千克售价、每千克成本与交易时间之间的关系分别如图1、图2所示(图1、图2中的图象分别是线段和抛物线,其中点P是抛物线的顶点).在这段时间内,出售每千克这种水果收益最大的时刻是_____ ,此时每千克的收益是_________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com