
科目: 来源: 题型:
【题目】老张用400元购买了若干只种兔,老李用440元也购买了相同只数的种兔,但单价比老张购买的种兔的单价贵5元.
(1)老张与老李购买的种兔共有多少只?
(2)一年后,老张养兔数比买入种兔数增加了2只,老李养兔数比买入种兔数的2倍少1只,两人将兔子全部售出,则售价至少为多少元时,两人所获得的总利润不低于960元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平行四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,且
,且![]() ,连接
,连接![]() ;
;
(1)如图![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(2)如图![]() ,连接
,连接![]() ,若
,若![]() ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图![]() 中所有面积等于
中所有面积等于![]() 的面积的钝角三角形.
的面积的钝角三角形.

查看答案和解析>>
科目: 来源: 题型:
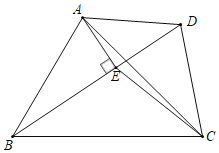
【题目】如图,在四边形ABCD中,tan∠ABC=![]() ,BD为对角线,∠ABD+∠BDC=90°,过点A作AE⊥BD于点E,连接CE,若AE=
,BD为对角线,∠ABD+∠BDC=90°,过点A作AE⊥BD于点E,连接CE,若AE=![]() DE,EC=DC=5,则△ABC的面积为_____.
DE,EC=DC=5,则△ABC的面积为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲车与乙车同时从A地出发去往B地,如图所示,折线O﹣A﹣B﹣C和射线OC分别是甲、乙两车行进过程中路程与时间的关系,已知甲车中途有事停留36分钟后再继续前往C地,两车同时到达C地,则下列说法:①乙车的速度为70千米/时;②甲车再次出发后的速度为100千米/时;③两车在到达B地前不会相遇;④甲车再次出发时,两车相距60千米.其中正确的有( )
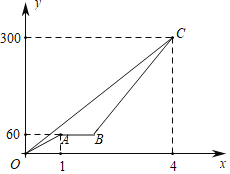
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
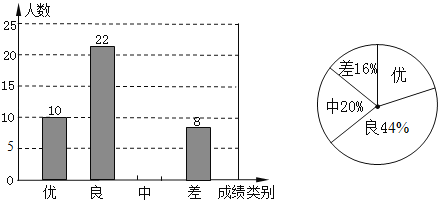
【题目】为迎接2016年中考,某中学对全校九年级学生进行了一次数学模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题:
(1)这次调査中,一共抽取了多少名学生?
(2)求样本中表示成绩为“中”的人数,并将条形统计图补充完整;
(3)该学校九年级共有1000人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目: 来源: 题型:
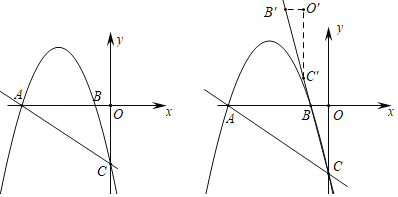
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2﹣
x2﹣![]() x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
(1)求直线AC的解析式;
(2)点P是直线AC上方抛物线上的一动点(不与点A,点C重合),过点P作PD⊥x轴交AC于点D,求PD的最大值;
(3)将△BOC沿直线BC平移,点B平移后的对应点为点B′,点O平移后的对应点为点O′,点C平移后的对应点为点C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,求出所有符合条件的点S的坐标.
查看答案和解析>>
科目: 来源: 题型:
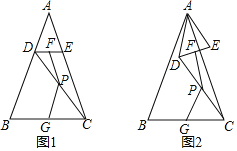
【题目】如图1,在△ABC中,AB=AC,∠BAC=α,点D、E分别在边AB、AC上,AD=AE,连接DC,点F、P、G分别为DE、DC、BC的中点.
(1)观察猜想:图1中,线段PF与PG的数量关系是 ,∠FPG= (用含α的代数式表示)
(2)探究证明:当△ADE绕点A旋转到如图2所示的位置时,小新猜想(1)中的结论仍然成立,请你证明小新的猜想.
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=2,AB=6,请直接写出PF的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
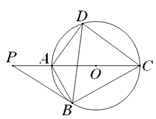
【题目】如图,点P是圆O直径CA延长线上的一点,PB切圆O于点B,点D是圆上的一点,连接AB,AD,BD,CD,∠P=30°.
(1)求证:PB=BC;
(2)若AD=6,tan∠DCA=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市为了销售一种新型“吸水拖把”,对销售情况作了调查,结果发现每月销售量y(只)与销售单价x(元)满足一次函数关系,所调查的部分数据如表:(已知每只进价为10元,销售单价为整数,每只利润=销售单价﹣进价)
销售单价x(元) | 20 | 22 | 25 | … |
月销售额y(只) | 300 | 280 | 250 | … |
(1)求出y与x之间的函数表达式
(2)该新型“吸水拖把”每月的总利润为w(元),求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com